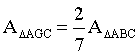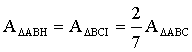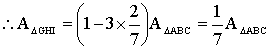Snow White and the seven dwarfs
Snow White makes a rainbow cake of the shape of a scalene triangle, that is, a triangle with three unequal sides. Grumpy, one of the seven dwarfs, is easily annoyed and complains a lot. He wants exactly one-seventh of the cake, no more and no less. How can Snow White cut 1/7 of the cake and gives it to Grumpy? Snow White makes 3 cuts starting from the three vertices of the triangle. Grumpy takes the middle portion. The other six dwarfs are happy to take any piece of the remaining cake.
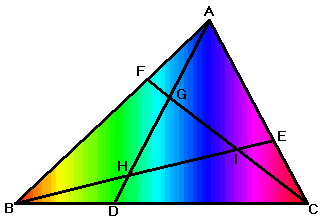
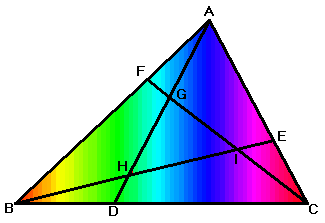
She cuts the rainbow cake using the following ratios: AF : FB = BD : DC = CE : EA = 1 : 2 Can you show that the middle portion GHI is 1/7 of the cake ABC?
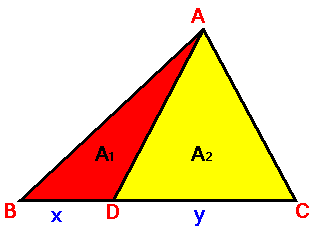
Hint 1 Too difficult. Never mind. This is the first hint. Theorem 1 x : y = A1 : A2 The proof is easy. The height of the triangles ABD and ADC are the same and the bases of the triangles are in ratio x : y.
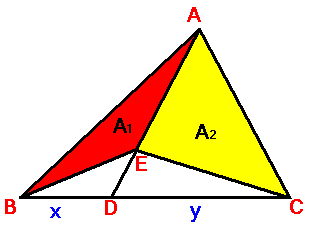
Hint 2 Still cannot solve. Here is more hint: Theorem 2 x : y = A1 : A2 Proof: By theorem 1 x : y = area of DABD : area of DADC = area of DEBD : area of DEDC A simple subtraction of areas gives the proof.
Hint 3 Life is easier if we simplify our problem. We remove one of the cuts and the remaining cuts are AD and CF. We like to find the ratio - area of DAGC : area of DABC.
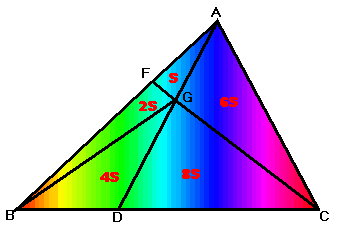
Join GB. Let the ADAFG = S (1) Since AF : FB = 1 : 2, By Theorem 1, ADFBG = 2S. ADAGB = ADAFG + ADFBG = 3S (2) Since BD : DC = 1 : 2 By Theorem 2, ADAGC = 2 ADAGB = 6S (3) Since AF : FB = 1 : 2 By Theorem 2, ADGBC = 2 ADAGC = 12S (4) Since BD : DC = 1 : 2 By Theorem 1, ADGBD : ADGCD = 1 : 2 \ ADGBD = 4S, ADGCD = 8S, ADGBC = ADGBD + ADGCD = 12S (5) ADAGC : ADABC = 6S : 21S = 2 : 7
Solution Similarly,