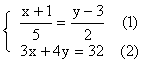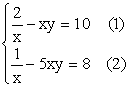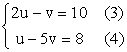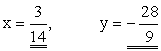Simultaneous Equation of two unknowns

Introduction

Besides the usual “Substitution” and “Elimination” methods, we can vary our techniques so as to find our solutions easier.

The coefficients of one variable in two given equations differ by ±1

Use addition or subtraction to get one variable with coefficient ±1. Then change the subject and substitute in one of the given equation.

Example

Solve: 3x + 5y = 17 (1)

2x – 3y = 1 (2)

Solution:

(1) – (2), x + 8y = 16

x = 16 – 8y (3)

Substitute (3) in (2), 2(16 – 8y) – 3y = 1

19 y = 31

y = 31/19 (4)

Substitute (4) in (3), x = 16 – 8(31/19) = 56/19

The difference of the coefficients of one variable in two given equations is the same (or opposite sign) as the difference of coefficients of the other variable

Use subtraction. Then change the subject and substitute in one of the given equation.

Example

Solve: 9x + 3y = 9 (1)

7x + 5y = -1 (2)

Solution:

(1) – (2), 2x – 2y = 10

x = 5 + y (3)

Substitute (3) in (1), 9(5 + y) +3y = 9

45 + 9y + 3y = 9

12y = - 36

y = -3 (4)

Substitute (4) in (3), x = 2

The sum of the coefficients of the two variables are the same

Sum first, then subtract.

Example

Solve: x + 9y = 57 (1)

9x + y = 33 (2)

Solution:

(1) + (2), 10x + 10y = 90

x + y = 9 (3)

(2) – (3), 8x = 24

x = 3 (4)

Substitute (4) in (3), y = 6

The constant term of the equations are the same

Equate the constant term, then eliminate variable or substitute.

Example

Solve: 4x - y = 110 (1)

9y - x = 110 (2)

Solution:

From (1) and (2), 4x – y = 9y – x

5x = 10y

x = 2y (3)

Substitute (3) in (1), 4(2y) – y = 110

y = 110/7 (4)

Substitute (4) in (3), x = 220/7

The coefficients of one variable in two given equations have a multiple relation in the two equations

Example

Solve: 3x – 4y = 7 (1)

9x – 10y + 23= 0 (2)

Solution:

From (1), 3x = 7 + 4y (3)

Substitute (3) in (2), 3(7 + 4y) –10y + 23 = 0

2y + 44 = 0

y = -22 (4)

Substitute (4) in (3), 3x = 7 + 4(-22) = -81

x = -27

One equation is a fractional equation

Example

Solve:

Solution:

From (1), Let:

Then x = 5k – 1, y = 2k +3 (3)

Substitute (3) in (2), 3(5k – 1) + 4(2k + 3) = 32

Solving, k = 1 (4)

Substitute (4) in (3), x = 4, y = 5

Change of variables

Some simultaneous equations seem NOT linear. By changing variables, you can make the equations linear.

Example

Solve: :

Solution:

Put

Then we get a pair of LINEAR equations with variables u, v :

From (4), u = 8 + 5v (5)

Substitute (5) in (3), 2(8 + 5v) – v = 10

9v = –6

Substitute (6) in (5),

Since

Therefore,

Solve for x and y, we get