3-4-5 Pythagorean triplet?
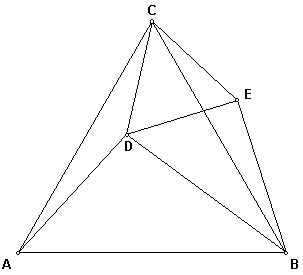
Question ABC is an equilateral triangle. CD = 3, AD = 4, BD = 5. Find ÐADC = x.
If you like to get the solution after trying, please scroll down…
Since BC = AC, we can construct DBCE º DACD as in the diagram. Since ÐBCE = ÐACD, ÐDCE = ÐACB = 60^o. But CD = CE, ÐCDE = ÐCED = 60^o. DCDE is equilateral. DE = CD = 3. EB = DA = 4 DB = 5 Since , ÐDEB = 90^o, by the converse of Pythagoras Theorem. ÐCEB = 60^o+ 90^o = 150^o. ÐADC = x. = ÐCEB = 150^o.