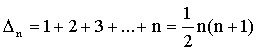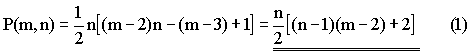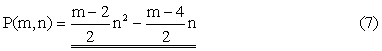Triangular Number , Square Number , Pentagon Number …. 

 

 

 

 
Triangular Numbers

Square Numbers

Pentagon Numbers

 

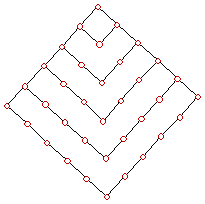
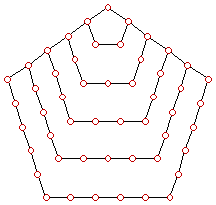
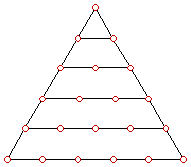
Polygon numbers

 

         The above diagrams show the geometric construction of polygon numbers. The formation of the first six terms of triangular numbers, square numbers, pentagon numbers are shown. You can extend to other polygon numbers. For triangular numbers, the first term is 1. The second triangular number is the number of points contained by the next larger triangle, that is 3. The third triangular number is 6, etc. It can be easily seen that the n-th triangular number, denoted by  Dn is given by

 

                        

How to find the value of other polygon numbers?

 

 

Table of Data

       The following table shows the value of the first ten values of the polygon numbers:

      

n =

1

2

3

4

5

6

7

8

9

10

m = 3

(Triangular)

1

3

6

10

15

21

28

36

45

55

m = 4

(Square)

1

4

9

16

25

36

49

64

81

100

m = 5

(Pentagon)

1

5

12

22

35

51

70

92

117

145

m = 6

(Hexagon)

1

6

15

28

45

66

91

120

153

190

m = 7

(Heptagon)

1

7

18

34

55

81

112

148

189

235

m = 8

(Octagon)

1

8

21

40

65

96

133

176

225

280

 

Construction of the table

 

(1)           The entries of the first column of the table are 1.

(2)           Write down the Triangle Numbers using Dn = 1 + 2 + … + n = (1/2)n(n + 1)

(3)           For Square Numbers, each number is the sum of the two triangle numbers, just on the top and top left. e.g.  9 = 3 + 6. (see the table on the top)

(4)           For Pentagon Numbers, each number is the sum of the Square number just on the top and the Triangular number just on top left. e.g.  51 = 36 + 15.

(5)           For Hexagon Numbers, each number is the sum of the Pentagon number just on the top and the Triangular number just on top left. e.g. 153 = 117 + 36.

(6)          You can continue in this way with Heptagon numbers.

 

But the question is: Can we find the general formula for all each numbers?

 

 

Calculation of Polygon Numbers

 

       Let   P(m, n)  be the nth value of the m-sided polygon number.

So, P(4, 3) is the third square number, that is, 9.  P(5, 6) is the sixth pentagon number, or 51.

 

       To begin with, the nth square number is given by:

               P(4, n) = 1 + 3 + … + (2n - 1)

We can calculate this sum simply by multiplying the number of terms by the average value of the terms.

Therefore, we get     P(4, n) = n (2n – 1 + 1)/2 = n2.

 

       Extending this method we can get:

               P(m, n ) = 1 + ( m – 1) + …. + [(m – 2)n – (m – 3)]

The last term needs some investigation and is left to the reader.

 

Multiplying the number of terms by the average value of the terms, we get:

      

 

 

Finite Difference

 

       Finite difference method is an interesting way to evaluate sequence of numbers. It is rather mathematical. Here are the simplified way procedures and more sophisticate calculations are omitted.

 

(1)          First we list the terms as a sequence of numbers, say, using the pentagon numbers:

                       1,     5,     12,   22,   35,   51,   70,   92, ….

 

(2)          Find the differences between successive terms until a constant is reached for every difference.

               (The differences of the terms are written on a line below)

 

                       1              5              12            22            35            51            70            92

                               4              7              10            13            16            19            22

                                       3              3              3              3              3              3

 

(3)          Count the number of times it was necessary to get a common difference.

               In this case, it is 2, and the common difference is 3.

 

(4)          The number of subtractions is the degree of the polynomial describing the sequence!

 

(5)          If you go through the polygon numbers, the degree of the polynomial needed is always 2.

               Therefore,

                       P(m, n) = an2 + bn + c                   (2)

 

(6)          The point is how to get a, b, c.

               The trick is the 0th, 1st and 2nd term of the mth polygonal number are:

                       0,  1,  m                              (Hala! we use the 0th term)

 

               From (2)

               P(m, 0) = a02 + b0 + c = 0     Þ    c = 0                       (3)

               P(m, 1) = a12 + b(1) + 0 = 1        Þ    a + b = 1                 (4)

               P(m, 2) = a22 + b(2) + 0 = m       Þ    4a + 2b = m            (5)

               Solving (3), (4), (5), we get:

 

                                        (6)

               Putting (6) in (2) we get:

 

                      

 

 

Further investigations:

 

(1)          Check that equations (1) and (7) are in fact the same formula for calculating polygon numbers.

 

(2)          By using substitution, check that the formula (1) or (7) can generate the table (or part of the table) above in the data part.

 

(3)          You can also find the polygon numbers by using the difference method in reverse. The first slant numbers are  1, m - 1, m – 2  for m-sided polygon numbers. You then start by adding numbers. For example, for octagon numbers, the first slant numbers are  1, 7, 6  and the third row with constant values of 6:

 

               1              8              21            40            65            96            133 …

                       7              13            19            25            31            37    ….

                               6              6              6              6              6      …