Paradox : All triangles are isosceles

“Proof”

In the diagram below, let DABC be any triangle. We like to prove that it is isosceles.

Let the angle bisector of ÐBAC and the perpendicular bisector of the side BC meet at point G.

Join GB, GC.

From G drop perpendicular lines GE and GF to the lines AC and AB respectively.

(1) BD = DC (construction)

ÐBDG = ÐCDG (right Ðs)

GD = GD (common)

DBDG @ DCDG (SAS) ….. (1)

(2) ÐFAG = ÐEAG (construction)

ÐAFG = ÐAEG (right Ðs)

ÐAGF = ÐAGE (Ð sum of D)

DAFG @ DAEG (ASA) ….. (2)

(3) BG = GC (corr. sides of @ Ds in (1))

GF = GE (corr. sides of @ Ds in (2))

ÐGFB = ÐGEC (right Ðs)

DGFB @ DGEC (RHS) ….. (3)

(4) AF = AE (corr. sides of @ Ds in (2))

FB = FC (corr. sides of @ Ds in (3))

AB = AF + FB = AE + FC

= AC

\ DABC is isosceles! Find the mistake.

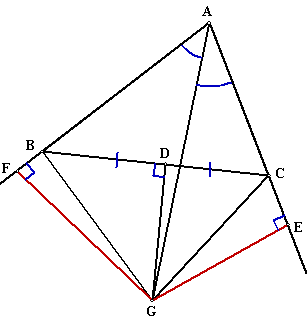
Perhaps you think that the angle bisector of ÐBAC and the perpendicular bisector of the side BC do not meet at a point inside the triangle. Good.

But then these two lines may meet at a point G outside the triangle as in the following diagram.