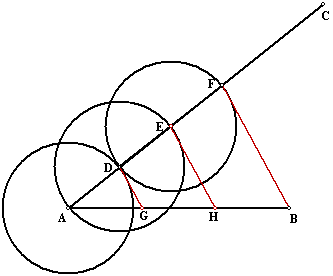How to construct a triangle given its three medians
Given a triangle ABC, it is easy to construct the three medians AP, BQ, CR by joining the vertices A, B, C to the corresponding mid-points of the opposite sides. However, can we do the opposite way. Given the lengths of the three medians AP, BQ, CR. Can we construct the triangle ABC? No problem. But first we should know some geometric facts.
Construction needs a pair of compasses and a ruler without any marks on it. First we should know how to trisect a given line segment AB. (You can extend this method to cut a given line segments into n equal parts) Draw a line AC at suitable angle with AB. Then use a pair of compasses to draw circles with any suitable radii, so that AD = DE = EF. Join BF. Then construct EH // FB and DG // FB. Then AG = GH = HB.
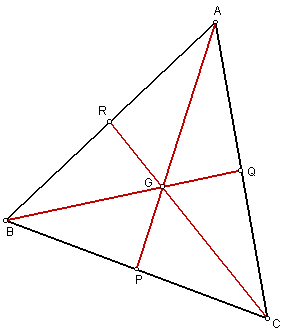
Medians cuts each other at a ratio of 2 : 1 We would like to show : AG : GP = BG : GQ = CG : CR = 2 : 1. There are many proofs, here is a geometric one. Produce GP to PS such that GP = PS. It is given that BP = PC. Since diagonals bisect each other, BGCS is a parallelogram. Since RG // BS and AR = RB, then AG = GS, by Intercept Theorem. \ AG = GS = GP + PS = 2GP Result follows.
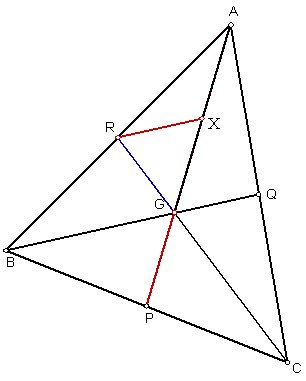
Now, we come back to our construction of triangle ABC, given the lengths of AP, BQ and CR. First we draw AP. Trisect AP and we can get G, X. Since AX = XG and AR = RB, we can get RX is half of BG, by mid point theorem. Finally we get RX is a third of BQ. RG is also a third of CR. The triangle GXR can be constructed since all three sides are well determined. Join AR and produce to a point B such that AR = RB. Also produce RG to a point C such that CR is of the given length. You can therefore get triangle ABC. Well done!