The use the Area to solve inverse proportion problem

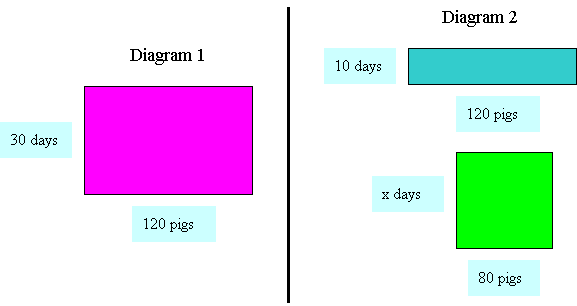
Question

A firm had enough food for 30 days for 120 pigs. If 40 pigs were sold after 10 days, the remaining food could last for how many days?

Solution

The following diagrams represent three pieces of "area of food" with pigs as length and days as width.

So you may imagine that certain number of pigs eat away certain piece of "area" in a number of days.

Let x be the number of days the remaining food could last.

In Diagram 1,

120 pigs eat away the red area in 30 days. Red "area" = 120 x 30 = 3600

In Diagram 2,

120 pigs eat away the blue area in 10 days. Blue "area" = 120 x 10 = 1200

After 10 days, there are (120 - 40) pigs, and they eat away the green "area" in x days.

Green "area" = (120 - 40)x = 80x

Since the pigs eat all "area" lastly in either of the ways shown in Diagram 1 or Diagram 2.

\ Red "area" = Blue "area" + Green "area"

\

3600 = 1200 + 80 x

Solving, we get x = 30

(Ans.) The remaining food could last for 30 days.

Lesson :

The idea of "Area", that is, pig-day is useful and this question is solved by setting up a pig-day equation.

Similar idea can be used to solve problems involving "man-hour" , "machine-day" ….