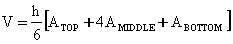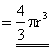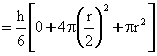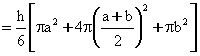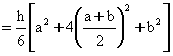A universal volume formula? |
|
|
The formula
For
most regular solids standing upright, you can use the following universal
formula for finding their volumes:
where h
is the height of the solid,
ATOP
is the cross sectional area
of the top of the solid,
AMIDDLE
is the cross sectional area of the middle of the solid,
ABOTTOM is
the cross sectional area of the bottom of the solid. |
|
|
Sphere h = 2r, ATOP = 0 AMIDDLE
= pr2 ABOTTOM = 0 \ Volume of Sphere
|
r
is the radius of the sphere |
|
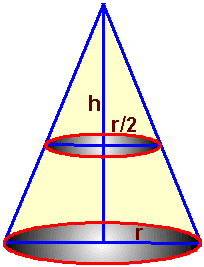
Cone h = height of cone, ATOP = 0 AMIDDLE
= p(r/2)2 ABOTTOM = pr2 \ Volume of Cone |
r
is the radius of the base of the cone |
|
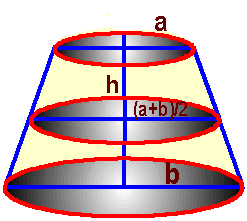
Conical frustum h = height of frustum, ATOP = pa2 AMIDDLE
= p[(a+b)/2]2 ABOTTOM = pb2 \ Volume of Conical Frustum |
a
is the top radius b
is the base radius |
|
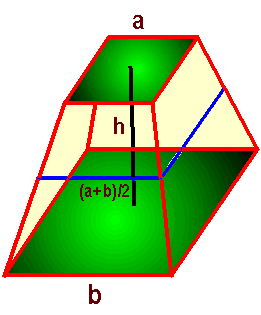
Square frustum h = height of frustum, ATOP = a2 AMIDDLE
= [(a+b)/2]2 ABOTTOM = b2 \ Volume of Square Frustum |
|
|
Harder exercise Can
you verify the formulas for the volumes of Conical Frustum and Square Frustum
by other method? |
|