Investigate the extremes |
|
|
One of the unconventional problem solving strategies
is to investigate the extremes of the problem. This method requires a rather
unusual way of thinking. You are going to modify variables that do not affect
the problem’s solution but make the problem considerably simpler. |
|
|
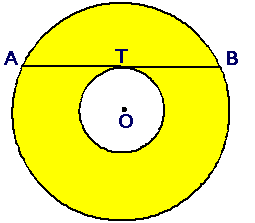
Question 1 The
tangent AB of the smaller of the two concentric circles is a chord of the
larger circle. Find the area of the region in yellow, if AB = 4. |
|
|
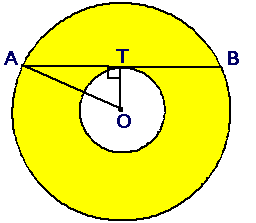
Traditional solution Let the radius of the big
circle be R and the radius of the small circle be r. Since AB is a
tangent, OT ^ AB. AB = 4, therefore AT = 2. By Pythagoras Theorem, OA2
= OT2 + AT2 \ R2 = r2
+ 22 \ R2 – r2
= 4 (1) Area of the region in
yellow = pR2 - pr2 =
p( R2
– r2) =
4p, by (1) |
|
|
“Investigate
the extreme” method Assume
the smaller circle is made smaller and smaller, and finally reduced to a
point. This can be done without loss of generality, and the problem remains
intact. Then AB becomes the diameter of the large circle. \ Area of the yellow region
= area of the larger circle = p(2)2
= 4p |
|
|
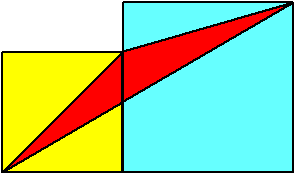
Question 2 Here is a more difficult
problem. There are two squares side
by side. The side of the yellow square is 2. Find the area of the red
triangle. |
|
|
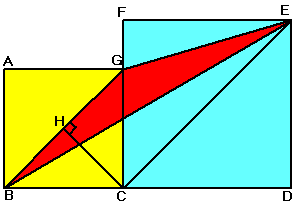
Traditional
solution Join CE. BG and CE are diagonals of
the adjacent squares. BG//CE. Now, consider DBGC and D BGE, The triangles have the
same base BG and between the parallel line BG and CE (They have the same
height CH) area of DBGC = area of DBGE \ Area of triangle in red = area of D BGE = area of DBGC = (1/2) BC2 =
(1/2)(2)2 = 2 |
|
|
“Investigate
the extreme” method Since
there is nothing given to the side of the blue square. The question is the same
by making the blue square smaller. Consider the extreme case by reducing the
blue square to a point, so that point E becomes point C. The area of the
triangle in red, that is, DBGE, becomes DBGC at once. Its area is
thus 2. |
|
|
Problem Imagine the earth is a
sphere. A rope A ties around the equator of the earth. Another rope B
circulates the equator but is 1 m above the ground. Guess the difference
in lengths of the two ropes A and B. Do you think that the difference is
longer then the height of the highest building in Hong Kong? (radius of Earth = 6 378.1 kilometers) Now do the calculations.
Can we use the “investigate the extreme” method? |
|