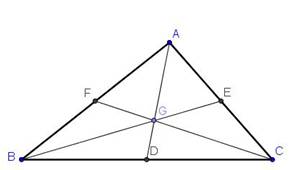
The centroid of a triangle divides each median in the ratio 2:1
The Theorem D, E, F are mid-points of BC, CA, AB. AD, BE and CF are medians. The medians cut each others are centroid G . We need to show that: AG : GD = BG : GE = CG : GF = 2 : 1
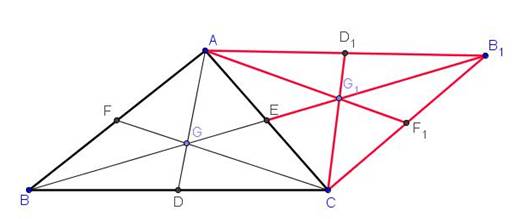
Simple Proof Reflect the triangle along AC, you can get a diagram below: ABCB1 is a parallelogram. BEB1 is a straight line . Since CD = AD1 and CD // AD1, DCD1A is a parallelogram. (opposite sides equal and parallel.) \ DG // CG1 Since BD = DC and DG // CG1 \ BG = GG1 (intercept theorem) BG : GG1 = 1 : 1 Since GE = EG1 , BG : GE = 2 : 1.