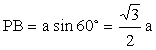The optimal bond angle of Methane
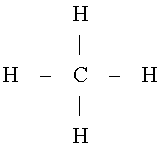
Introduction Methane molecule consists of one carbon and four hydrogen atoms (CH4). Lewis gave a planar structure for CH4 as shown on the left. This Lewis structure suggests that the optimal bond angle for methane is 90°. However, this two dimensional model is unsatisfactory.
Three dimensional model The figure in the left hand side shows a three dimensional model of methane. The central black ball represents the carbon (C) and four white balls are hydrogen atoms (H), forming a tetrahedron structure. In this article, we are going to show that the HCH covalent bond angles are 109.5°.
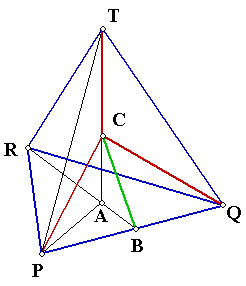
Let the carbon atom situated at C and four hydrogen atoms at P, Q, R, S. Let TA be the height of the tetrahedron. The optimal bond angle = Ðx \ Ðx = ÐTCP = ÐTCQ = ÐPCQ B is the mid point of PQ. ÐRBP = 90° Since PQR is equilateral, ÐPRA = ÐARP = 30° \ ÐPAB = 60° Let PA = a, we can get
Putting PC = y, and ÐPCB = Ð x / 2 From PC sin PCB = PB \ ÐPCT = Ð x, therefore ÐPCA = 180° - x PA = PC sin PCA \ a = y sin (180° - x) = y sin x (2) We now solve (1) and (2) for x, From (2), (3)/2x(1), x/2 » 54.74° x » 109.5°		Consider the right angled DPCB. Consider the right angled DPCA. We apply half-angle formula here. The fun is both y and a are cancelled!
Technique We employ the technique of setting two equations and solving simultaneous equations. If you cannot handle half-angle formula, you can still find the optimal bond angle. Fun to try!