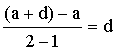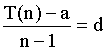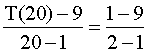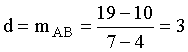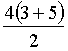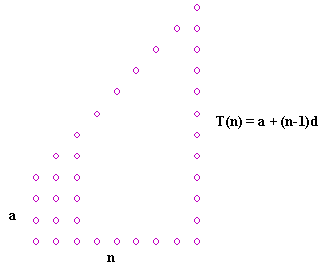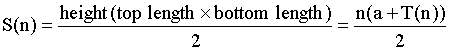|
Use of gradient
and area in arithmetic sequence and series |
||||
|
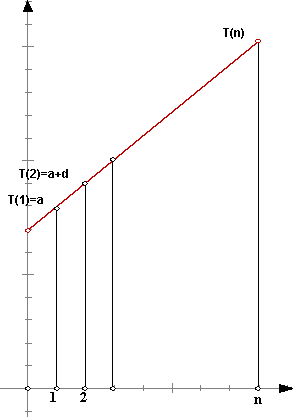
Gradient An arithmetic sequence is
characterized by having a common difference, d. Let T(1) = a be the first term, d be the common difference and T(n) be
the general term of an arithmetic sequence. Then d = T(2) – T(1) = T(3) – T(2) =
…. = T(n) – T(n-1) We like to draw as in the
diagram T(1) = a, T(2) = a +d , …., T(n). |
||||
|
|
||||
|
The coordinates of the top points of vertical lines are (1, a), (2,
a+d), ….. , (n,T(n)). By considering the gradient of the first two points,
Since the given sequence is arithmetic, the red line is straight with
gradient d. If we find the gradient of
the line using the first and the last point, (1, a) and (n,
T(n)), we get \ |
||||
|
Example 1
In the arithmetic
sequence 9, 1, -15, …. , find the 20th term. SolutionLet A(1,9), B(2,1) and
C(20, T(20)). The three points A, B, C
are collinear.
\ T(20) = - 143. |
||||
|
Example 2
Insert 6 arithmetic means between the numbers -18 and 3. Solution Consider the points A(1, -18) and B(8, 3). \ The 6 arithmetic means
are –15, -12, -9, -6, -3, 0. |
||||
|
Example 3
In the arithmetic sequence the fourth term is 10, the
seventh term is 19. Find the common difference
d and the 20th term Solution
Let A(4, 10), B(7, 19), C(20, T(20)) \ \ T(20) = 58. |
||||
|
Example 4
In the arithmetic sequence T(p) = q and T(q) = p, where p ≠ q. Find T(p+q). Solution Let A(p, q), B(q,p), C(p+q, T(p+q)). A, B and C are collinear. \ Solving, we get T(p+q) = 0. |
||||
|
Area
We can use “area” formulae
for calculating the numbers of dots in the diagrams: (1)
Applying the “area” of rectangle: Number of dots = 3 x 4 = 12 |
|
|||
|
(2)
Applying the “area” of trapezium, Number of dots = = 16 |
|
|||
|
As we can see, the formulae
of area of triangle, rectangle, trapezium etc can be used in counting the
number of dots if the dots are arranged in a lattice pattern. Let S(n) = T(1) + T(2) +
… + T(n) be the sum of the terms of the arithmetic sequence and we get an
arithmetic series. Now, study the
diagram in the right: The first vertical column
of dots represents T(1). The last vertical column
of dots represents T(n). There are altogether n
columns. |
|
|||
|
S(n) is the sum of all columns
of dots and we can apply the area formula for trapezium. \ \ |
||||