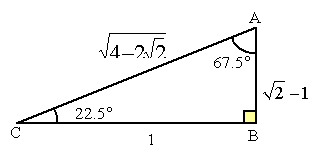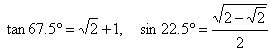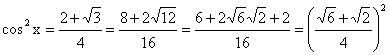Special angles by solving equations
tan 22.5° Let x = 22.5° 2x = 45° tan 2x = tan 45° = 1 tan^2 x + 2 tan x – 1 = 0 By quadratic equation formula, we get (The negative root was rejected since tan x > 0)
More … Since we draw a DABC right angled at B, ÐC = 22.5°, ÐA = 67.5° .
The hypotenuse AC can be found using Pythagoras Theorem: From this triangle we can read more trigonometric functions of special angles. For examples, after some rationalization exercise, we get:
cos 15° Let x = 15° 2x = 30° Since cos x > 0, We can draw a triangle with A = 75°, B = 90°, C = 15° and read more trigonometric functions involving 15° and 75°.
sin 18° Let x = 18° 5x = 90° 3x = 90° - 2x (This step is crucial as multiple angle with 5x is complicate) cos 3x = cos (90° - 2x) = sin 2x (1) 4 cos^3 x – 3 cos x = 2 sin x cos x Since cos x ¹ 0, divide the above by cos x, 4 cos^2 x – 3 = 2 sin x 4(1 – sin^2 x) – 3 = 2 sin x 4 sin^2 x + 2 sin x – 1 = 0 (2) By using the quadratic equation formula and rejecting the negative root, we have:
Exercise (1) Instead of taking cosine as in equation (1) above, we take sine: sin 3x = sin (90° - 2x), can we find sin 18°? (Hint: Factor Theorem) (2) Can you use equation (3) to show: