Proofs of Sine Law

Height of triangle

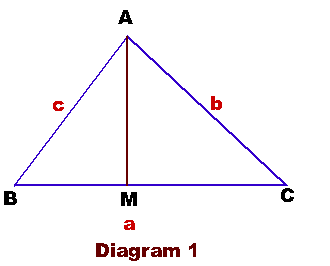
In Diagram 1,

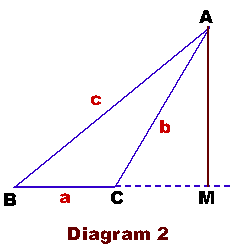
If C is acute, the altitude from point A to BC is given by h_a = AM = b sin C

In Diagram 2,

If C is obtuse, we still get h_a = AM = b sin (180° - C) = b sin C

Similarly, if you consider angle B, you get h_a = c sin B

Dropping altitudes from B to CA and C to AB, we get the following equalities:

h_a = b sin C = c sin B

h_b = c sin A = a sin C

h_c = a sin B = b sin A

We can get the Sine Law easily from these equalities:

Area of the triangle

Area of the triangle = D

Consider this formula cyclically, we have:

We can get the Sine Law rearrangement:

Circle

If you know some theorems involving circle, the proof of Sine Law is more interesting.

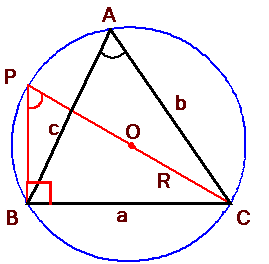
You can draw a circle passing through the vertices of the DABC.

This circle is called the circum-circle. Let O be the center of the circle.

Join CO and produce to meet the circle again at P. Join PB.

PC = 2R (Diameter of the circle)

ÐPBC = 90° (Ð in semi-circle)

ÐP = ÐA (Ð in same segment)

By considering other angles of the triangle, we get:

Sine Law

In conclusion we have the Sine Law, written as:

where D is the area of the triangle ABC

and R is the radius of circumcircle passing through A, B, C.

Also, note that Sine Law can be written in ratio form:

sin A : sin B : sin C = a : b : c