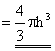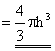Lord of rings ? |
|
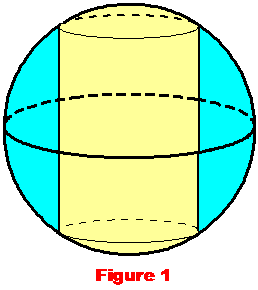
A magic ring is made by cutting the sphere
in Figure 1 by drilling a cylindrical hole (together with the top and bottom
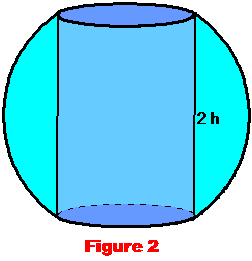
caps). The ring is shown in Figure 2. The only given is that the
cylinder is of height 2h. What is the volume of this magic ring?
|
|
Analysis Since
the radius of the sphere and the radius of the cylinder are not given, it
seems that the volume of the magic ring cannot be found. |
|
Calculation
Let R be the radius of the
sphere. We don’t know R, but we like to carry on. The sphere is got by
rotating the circle: C: x2 + y2
= R2 about the
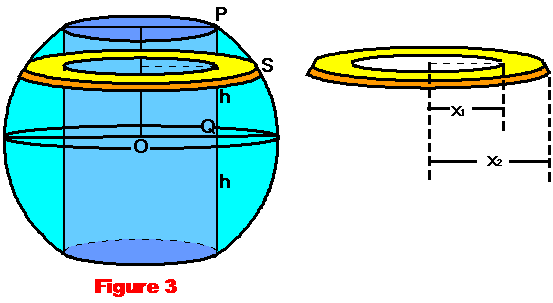
y-axis. Let x1 be the inner radius (of
the cylinder) and x2 be the outer radius (of the sphere) of the elementary
disc as shown in the yellow part of Figure 3. The thickness of the disc is
dy. Volume of the magic ring Now, x2 is
coming from the sphere by rotating the circle C and therefore x22
= R2 – y2
(2) Also, x1 is
coming from the cylinder, which is constant at different height of the
cylinder. x12
= OQ2 = OP2 – PQ2 = R2 – h2 (3) Substituting (2), (3) in
(1), we get: You can then see the final
answer is independent of R, the radius of the sphere. Haha! The volume of the
magic ring can be found! |
|
Quick solution Since
the question gives you only the height (2h) of the ring and not the radius of
the cylinder. Therefore we can put the radius of the cylinder tending to 0.
Since there is nothing cut away, the magic ring becomes a sphere. This sphere
has diameter equal to the height of the cylinder 2h. The radius of the sphere
is thus h. By
the sphere formula, the volume of the magic ring |
|
Final
discussion (1) There
are two things that needs consideration for any solution to a problem: There
is no problem for "existence". Fine. the
quick solution is perfect. But
there are sometimes many solutions to one problem.... (2) If
the radius of the sphere is bigger, the cylindrical hole is also bigger. However,
the volume of the magic ring is unchanged! You
can draw two diagrams with different radii of the sphere. Compare
and see what happens. |