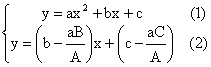Solve a quadratic equation by using any quadratic graph
The Problem Suppose you are given the graph: y = x^2 – 2x – 4 as in the L.H.S. You are required to solve the quadratic equation: 2x^2 – 3x – 6 = 0 by drawing a straight line.
Solution We begin with 2x^2 – 3x – 6 = 0, Divide both sides by 2, x^2 – 1.5x – 3 = 0 x^2 = 1.5x + 3 \ x^2 – 2x – 4 = 1.5x + 3 – 2x – 4 = – 0.5x –1 Let y = x^2 – 2x – 4 and y = – 0.5x –1 Therefore all we have to do is to draw the straight line y = – 0.5x –1. The intersection of the given graph y = x^2 – 2x – 4 and this straight line is the solution. The graphs are shown below.
The L.H.S. shows that the intersection points are: (-1.1, -0.3) and (2.6, -2.3) Therefore the roots of the equation: 2x^2 – 3x – 6 = 0 are x = -1.1 and x = 2.6 (to 1 dec. place)
The general case In fact, if we are given any quadratic graph: y = ax^2 + bx + c We can solve any quadratic equation: Ax^2 + Bx + C = 0 by drawing only a straight line! We begin with: Ax^2 + Bx + C = 0 Divide by A and multiply by a, we get: (1) is the given quadratic graph and (2) is the straight line graph you need to draw. The intersection(s) of these two graphs is/are the root(s) of the equation: Ax^2 + Bx + C = 0. Note: If there is no intersection point, the equation: Ax^2 + Bx + C = 0 has no real roots.