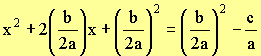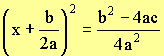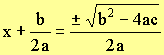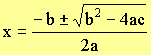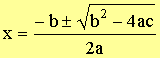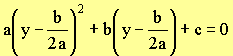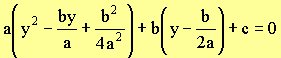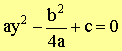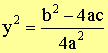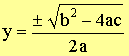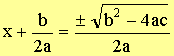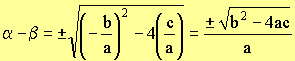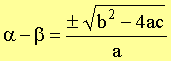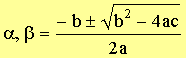Quadratic Equation Formula
|
Method
mentioned in most textbook |
|
The given quadratic equation
|
|
Move c to the right hand side
|
|
Divide by a
|
|
Add a term to both sides for
completing square
|
|
Complete square,
Join the terms on right hand side
|
|
Take square root
|
|
Solve for x
|
|
|
Sridhara’s
Method (circa 1025 A.D.) |
|
The given quadratic equation
|
|
Move c to the right hand side
|
|
Multiply by 4a
|
|
Add
|
|
Complete square,
Join the terms on right hand side
|
|
Take square root
|
|
Solve for x
|
|
|
Vieta’sMethod
(circa 1540 A.D.) |
|
The given quadratic equation
|
|
Substitute
|
|
Expand
|
|
Simplify
|
|
Move terms
|
|
Take square root
|
|
Change y to x
|
|
Solve for x
|
|
|
Why we use the substitution :
|
|
The given quadratic equation
|
|
Substitute x = y + d
|
|
Expand and group terms
|
|
|
We don’t
need the y-term, we therefore put the coefficient of y zero |
2ad + b = 0
|
|
Harriot’s
Method (circa 1630 A.D.) |
|
The given quadratic equation
|
|
Divide by a
|
|
Let a, b are roots, then the quadratic equation is the
same as :
|
|
Comparing coefficients of quadratic
equations (1) & (2)
|
|
Consider the identity
|
|
Find a - b
|
|
We have two equations in
a + b, a - b
|
|
Solve for a , b
|
|