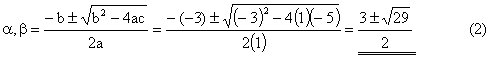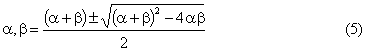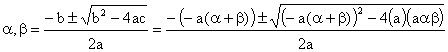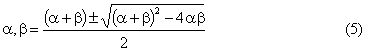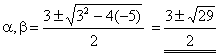A formula for quadratic equation |
|
Problem If a, b are roots of a quadratic
equation and the values of a + b, ab are given, find a, b. |
|
Example Given a + b = 3, ab = –5, find a, b. Solution The quadratic equation with a + b = 3, ab = – 5 is x2 – 3x – 5 =
0 (1) Solve (1) using quadratic
equation formula, we get: |
|
General formula Can we find a general formula (without
finding the quadratic equation and solve the quadratic equation as in the
above example) ? |
|
Solution (1) First
we note: (a– b)2 = (a + b)2 - 4ab Therefore we have: or Although we have a “±” sign in (3) and another “±” in (4), we need only one
“±” in (5). We also understand that
even if a + b, ab are real numbers, a and b can be complex number. (2) We
can also get (5) by Vieta’s Theorem: \ b = –a(a + b), c = aab Substitute these
equations in the quadratic equation formula, we have: Simplify and cancel “a”
in both numerator and denominator, we get: |
|
The problem again Given a + b = 3, ab = –5, find a, b. From (5), we get: |