To construct a square with area equal to a given polygon
Step 1 Firstly we like to construct a triangle with area equals to the area of a given quadrilateral. The method mentioned here can be extended to any other polygons. For example, a pentagon can be reduced to a quadrilateral with equal area.
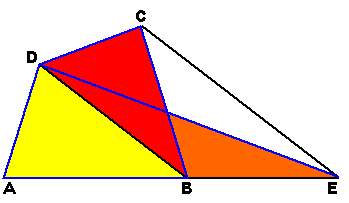
Given a quadrilateral ABCD. 1. Join BD. 2. Draw a line through C parallel to DB. 3. Produce AB to meet the line in 2 at E. 4. Join DE. 5. Then DAED is of equal area to ABCD.
Reasons: For DDBC and DDBE, they both have the same base DB. They also have the same height since they are between two parallel lines DB and CE. Therefore, area of DDBC = area of DDBE Area of quadrilateral ABCD = area of DABD + area of DDBC = area of DABD + area of DDBE = area of DAED
Step 2 We like to construct a rectangle equal in area to a given triangle. We use the same triangle produced in Step 1, that is, DAED, for demonstration.
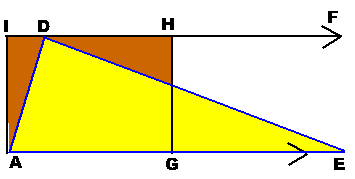
Given DAED, 1. Draw a line through D and parallel to AE. 2. Bisect AE at G. 3. From G construct a line perpendicular to AE and meet the line in 1 at H. 4. From A construct a line perpendicular to AE and meet the line in 1 at I. 5. Then the area of rectangle AGHI is equal to the area of DAED.
Reasons: Base of the rectangle is equal to half of the base of the triangle. The height of the rectangle is equal to the height of the triangle.
Step 3 Finally we have to construct a square of area equal to the area of a given rectangle. We use the same rectangle produced in Step 2, that is, AGHI.
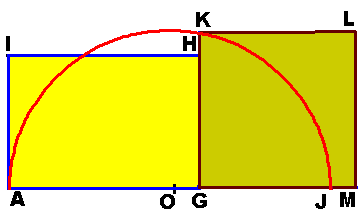
Given rectangle AGHI, 1. Produce AG to J such that GJ = GH. 2. Find the mid point O, of AJ. 3. Use O as center, OA as radius, draw a semi-circle. 4. Produce GH to meet the semi-circle at K. 5. Use GK as side, construct a square GKLM. 6. Area of AGHI = Area of GKLM.
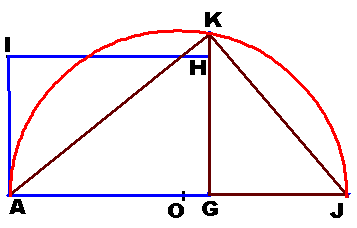
Reasons: As in the left diagram, ÐAKG = 90° (Ð in semi-circle) ÐKAG = 90° – ÐAKG = ÐGKJ \ DAGK ~ DKGJ (AAA) AG/GK = KG/GJ AG ´ GJ = KG^2 AG ´ HG = KG^2 \ Area of AGHI = Area of GKLM.