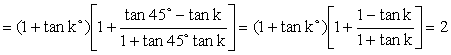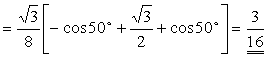Find a partner

Sometimes it is interesting to find a “partner” in proving trigonometric identities or evaluating trigonometric functions. The calculations are then easier.

Example 1

Find the value of sin² 10° + cos² 40° + sin 10° cos 40°.

Solution

Let x = sin² 10° + cos² 40° + sin 10° cos 40°

y = cos² 10° + sin² 40° + cos 10° sin 40°

then x + y = 2 + sin 50°

x – y = cos 80° - cos 20° - sin 30° = -2sin 50°sin 30° - 1/2

= - sin 50° - 1/2

Adding and divide by 2, we get x = 3/4

Example 2

Find the value of sin 10° sin 30° sin 50° sin 70°.

Solution

Let x = sin 10° sin 30° sin 50° sin 70°

y = cos 10°cos 30°cos 50°cos 70°

then xy = (sin 20° sin 60° sin 100° sin 140°)/16, using sin 2q = 2 sin q cos q

= (sin 20° sin 60° sin 80° sin 40°)/16

= (cos 70° cos 30° cos 10° cos 50°)/16

= y/16

Since y ¹ 0, cancel y on both sides, we therefore have x = 1 / 16

Point to study : How do you evaluate y? (see bottom of this page for solution)

Example 3

Solution

Let x = cos q cos 2q cos 4q … cos 2ⁿq

y = sin q sin 2q sin 4q …. sin 2ⁿq

(in the above, the power for 2 is (n+1) because the index of n “runs through” 0 to n)

Since y ¹ 0, canceling the y on both sides, we get:

Example 4

Find the value of:

(1 + tan 1°)(1 + tan 2°)…. (1 + tan 44°)

Solution

Let x = (1 + tan 1°)(1 + tan 2°)…. (1 + tan 44°)

then x = (1 + tan 44°)(1 + tan 43°)…. (1 + tan 1°)

Multiply, we get:

x² = [(1 + tan 1°)(1 + tan 44°)][(1 + tan 2°)(1 + tan 43°)]…[(1 + tan 44°)(1 + tan 1°)]

Since (1 + tan k°)[1 + tan (45°-k°)]

\ x² = 2⁴⁴

\ x = 2²².

Challenge

Show that:

tan q + 2 tan2q + 4 tan 4q + …. + 2ⁿ tan(2ⁿq) = cot q - 2ⁿ⁺¹cot(2ⁿ⁺¹q).

Solution for point to study:

cos 10°cos 30°cos 50°cos 70° = (cos 10° cos 70°) cos 30°cos 50°