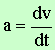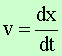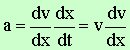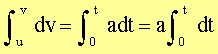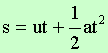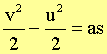Newton’s Laws of Motion
Derivatives (1) (2) (3)	We consider the acceleration, a, to be a constant. We like to get three differential equations. Acceleration is the rate of change of velocity, that is, the derivative of velocity with respect to time. Velocity is the rate of change of distance x, or the first derivative of distance with respect of time. We can use the Chain rule for getting the differential equation (3).
From (1), we get: dv = a dt On integrating both sides, we get: \ v – u = at \ v = u + at (4)	In the definite integral on L.H.S., the lower limit, u, is the initial velocity and the upper limit, v, is the final velocity. And on the R.H.S., the upper limit, t, is the total time the particle traveled and the initial time is t = 0. Equation (4) is the First law of motion.
From (2) and (4), we get: dx = (u + at) dt On integrating both sides, we get: \ \ (5)	The upper limit of the left integral, s, is the total distance the particle traveled. The initial distance is zero. The upper limit of the right integral is the total time. u and a are constants here. Equation (5) is the Second law of motion.
From (3) above, v dv = a dx On integrating both sides, we get: \ (6)	On the L.H.S., the upper limit, v, is the finial velocity and the lower limit, u, is the initial velocity. Equation (6) is the Third law of motion.
Note (1) The acceleration, a, is considered to be constant. In general this is not the case. If acceleration is not constant, the Laws of motion (4), (5) and (6) do NOT hold. (2) We use Definite Integrations in getting the results. You can also use Indefinite Integrations. But then you have to handle the integrating constants generated using initial conditions.