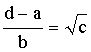Why there is infinite number of Irrational Numbers? |
|
Introduction We know that there is infinite
number of rational numbers. However, it is true that there is infinite number
of irrational numbers? We can give a few examples such as Ö2, log 2,… In fact, there is infinite
number of them. Using more sophisticate mathematics, the number of irrational
numbers is even more than rational numbers! |
|
Algebra If Ö2 is irrational, we may
think that 2Ö2, 3Ö2,… are also irrational,
and perhaps 1+Ö2, 2+Ö2,… are also irrational. Instead of proving the numbers
are irrational one by one, we employ a powerful tool called algebra! We like
to prove that all numbers of the form a + b(Öc) are irrational, where a, b are rational numbers
and Öc is
irrational. |
|
Proof
We use an interesting kind of
proof : Proof by Contradiction. Assume that a + b(Öc) is rational, Then d = a + b(Öc), where d is rational. The left hand side is
rational, since d, a, b are rational. But the right hand side is irrational. Therefore there is a
contradiction and a + b(Öc) is irrational. |
|
More irrationals We therefore know that adding,
subtracting, multiplying and dividing an irrational number by a
rational number is still irrational. Is it true that the square root
of an irrational number is still irrational? For example: is still irrational. The proof is left to the reader. |