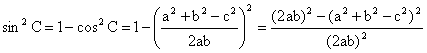Heron’s Formula |
|
|
Area of triangle Heron’s formula is used to
find the area of a triangle ABC. Let the sides of the
triangle opposite to the vertices A, B, C be a, b, c. Let the semi-perimeter be: Then the area of DABC |
Heron of Alexandria
|
|
Proof The proof of Heron’s
formula is a good exercise of trigonometry (or geometry) and algebra. Here is a proof: The formulas we use are: (1) Area of triangle: (2) Cosine Law: (3) Square relation: sin2
C + cos2 C = 1 From (3) and (2),
From (1), |
|
|
Verifications You may wish to verify
Heron’s formula for the following special cases: (1) A right-angled triangle
with sides 3, 4, 5. (2) An equilateral triangle
with sides a, a, a. |
|