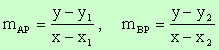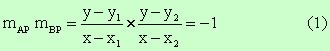Diameter Form of a circle
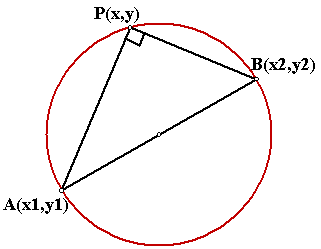
The Diameter Form Formula Let be the ends of the diameter of a circle. Let P(x, y) be any point on the circle. The gradients, Since ÐAPB is a right angle (Ð in semi-circle), We get the equation of the circle:
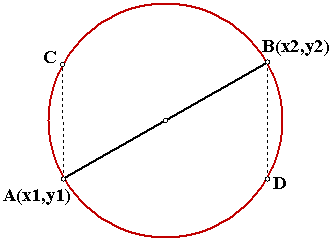
The Pitfall Equation (1) is not a complete circle. It is a circle with four “holes” A, B, C, D. (Two holes if the diameter is perpendicular or parallel to the x-axis). The reason is that if x = x1 or x = x2, the denominator of the left hand side of (1) is equal to zero, making the equation undefined. Points A and C have the first coordinates x1. Points B and D have the first coordinates x2.
Vectors For students who know vector operations can get the Diameter Form easier: Since ÐAPB is a right angle (Ð in semi-circle), \
Exercise 1. Since ÐAPB is a right angle, can you use the Pythagoras Theorem to get the Diameter Form of the circle? Can you simplify to get (2) again? 2. Can you find the mid-point of the diameter AB? This is the center of the circle. Can you find the radius of the circle? Use the Center-radius Form of the circle to find the Diameter Form. (equation (2))