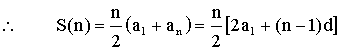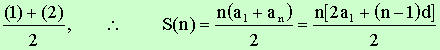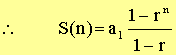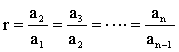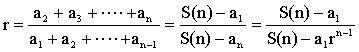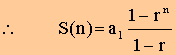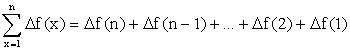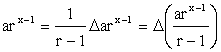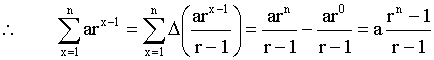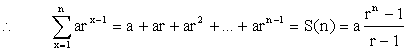On Arithmetic Series and Geometric Series

In proving the formulas of the sums of an arithmetic or geometric sequences,

the following non-conventional methods worth studying :

Arithmetic series

Let the arithmetic series be a₁, a₂, …., a_n with a common difference, d.

The arithmetic mean of the first n terms is equal to the arithmetic mean of the first and last terms.

That is:

Arithmetic series

Let the arithmetic series be a₁, a₂, …., a_n with a common difference, d.

(Please investigate the reasoning for equation (2) below)

S(n) = a₁ + (a₁ + d) + (a₁ + 2d) + ……. + [a₁ + (n-1)d] (1)

S(n) = a_n + (a_n - d) + (a_n - 2d) + ……. + [a_n - (n-1)d] (2)

Geometric series

Let the geometric series be a₁, a₂, …., a_n with a common ratio, r. (r ¹ 1)

S(n) = a₁ + a₁r + a₁r² + …. + a₁r^n-1

S(n-1) = a₁ + a₁r + a₁r² + …. + a₁r^n-2

We can see that :

S(n) - S(n-1) = a₁r^n-1 (1)

S(n) – r S(n-1) = a₁ (2)

The above is a simultaneous system of equations with 2 unknowns S(n) and S(n-1).

We can then solve for S(n).

Consider (2) – r(1), we get for r ¹ 1,

Geometric series

Let the geometric series be a₁, a₂, …., a_n with a common ratio, r. (r ¹ 1)

Then,

By the Equal Ratio Theorem,

rS(n) – a₁rⁿ = S(n) – a₁

S(n) [1 – r] = a₁ [1 – rⁿ]

Difference Method

For more mathematical mature readers, the employment of first order difference method
in getting the formula for geometric series is interesting.

We define the difference operator: Df(x) = f(x + 1) – f(x)

Then we have the following elementary properties:

1. For any constant k , D k f(x) = k f(x + 1) – k f(x) = k [f(x + 1) – f(x)]

2.

Now, Dar^x-1 = ar^x – ar^x-1 = ar^x-1 (r – 1)

If r ¹ 1, then we get

, by property (1) above.

Using property (2), we have:

Writing the summation in full, we finally get:

Readers interested in learning more on difference method may consult some advanced algebra books.