Reading angles as arcs!

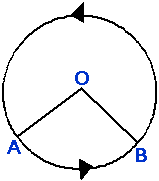
Definition

It is interesting to read angles as arcs. But first we have some agreement. In order to write arcs easily we use the anti-clockwise direction. We define:

ÐAOB » arc AB

reflex ÐAOB » arc BA

Note :

(1) arc AB ¹ arc BA

(2) The symbol “»” is not equality but only “supposed to be equivalent to”

(3) We use the same symbol for backward operation, i.e.

arc AB » ÐAOB

There are five common types of angles connected with theorems on circles. They are listed below as arcs. Do you know why they are defined like that? Find out yourselves. Hint for (3) below: exterior angle of triangle.

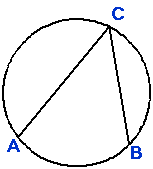
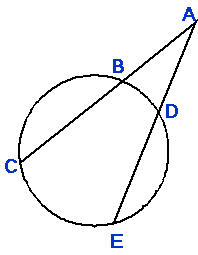
(1) Angle at circumference

ÐACB » ½ arc AB

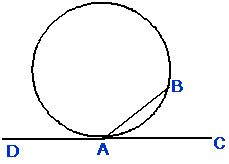
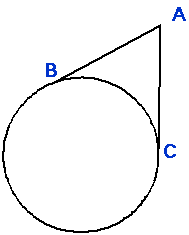
(2) Tangent angles

ÐBAC » ½ arc AB

ÐBAD » ½ arc BA

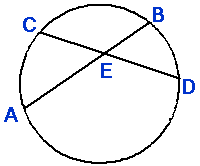
(3) Intersecting chords

ÐAED » ½ (arc AD + arc BC)

ÐBED » ½ (arc CA + arc DB)

(4) Chords intersect outside circle

ÐCAE » ½ (arc CE - arc DB)

(5) Two tangent lines

ÐBAC » ½ (arc BC - arc CB)

Purpose

The purpose of defining like this is to read angles as if they are arcs.

Can you draw diagrams to show some of the theorems on circle?

Old theorems	New look (not really a proof)
Angles in same segment	both angles » ½ the same arc
Opposite angles of cyclic quadrilateral	sum of opposite angles » sum of opposite arcs which is a circle = ½ (360°) = 180°
Angle in alternate segment	both angles » the same arc

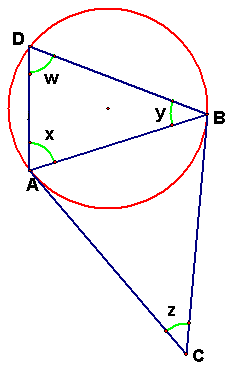
Example 1

In the right diagram, CA and CB are tangents to the circle. Find z in terms of x and y.

Solution

z » ½ (arc BA – arc AB)

» ½ (arc BD + arc DA – arc AB)

» x + y – w

= x + y – (180° - x – y)

= 2(x + y) – 180°

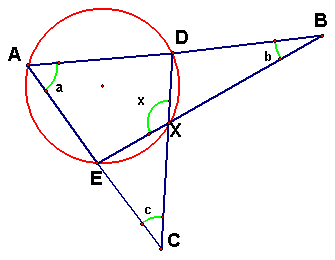
Example 2

In the figure in the right,

ADB, AEC, CXD, BXE are straight lines.

A, E, X, D are concyclic.

Find x in terms of a, b, c.

Solution

b » ½ (arc AE – arc XD) (1)

c » ½ (arc DA – arc EX) (2)

(1) + (2),

b + c » ½ [arc AE + arc DA – (arc XD + arc EX)]

= ½ [arc DE – arc ED]

» x – a

\ x = a + b + c

Conclusion

Although reading angles as arcs technique seems not a standard way in proving circle problems, it is very helpful especially in multiple-choice questions.