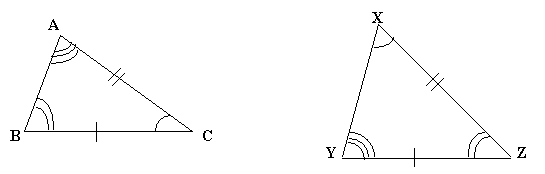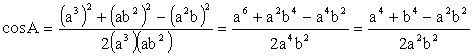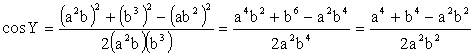Almost Congruent Triangles

Given two triangles ABC and XYZ and you have three pairs of angles and three pairs of sides. How is it possible for two triangles to be identical in five respects of these six quantities, and yet not to be congruent ?

Geometry

Readers after studying a bit on elementary geometry may know that there are four types of checking the congruence of two triangles : RHS , SSS, SAS and ASA.

For SSA or AAS cases further careful checking is usually needed.

As in the above diagrams, we can see that DABC and DXYZ are not congruent, but they have three pairs of angles and two pairs of sides are equal.

Trigonometry

The problem seems to have solved, but what really are the relationship between the sides and the angles.

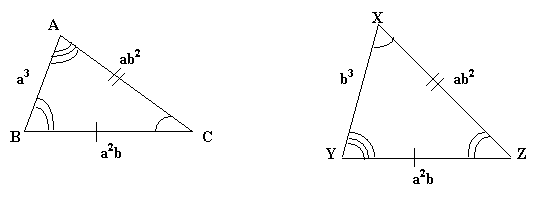
The solution is given in the above diagrams where

AB = a³ , BC = a²b , CA = ab².

XY = b³, YZ = a²b , ZX = ab².

Now, with different values of a and b , we have two pairs of sides in the two triangles are equal, that is BC = YZ and CA = ZX .

It leaves to look at the angles.

By Cosine Law, we get:

\ ÐA = ÐY

Can you check that : ÐB = ÐZ and ÐC = ÐX ?