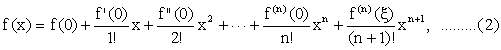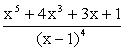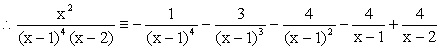Application of Taylor theorem to polynomial and partial fraction |
|
Taylor’s theorem Let aÎR, f(x) be a function that is continuous with its first (n + 1) derivatives on an interval containing a and x. Then where the remainder: A useful special case in
which a = 0 is called the Maclaurin series: where x lies between 0 and x. |
|
Partial Fraction Very often the Taylor’s theorem is used to expand infinite series such as sin x or ex. However, it can be applied to functions that can be expanded finitely. You may then find the theorem very useful in dealing with polynomials or partial fractions. |
|
Example 1 Express x5
+ 4x3 + 3x + 1 as a polynomial with variable (x – 1). Solution Let f(x) = x5 + 4x3
+ 3x + 1, then f(1)
= 9 f’(x) = 5x4
+ 12x2 + 3x, f’(1)
= 20 f(2)(x)
= 20 x3 + 24x, f(2)(1)
= 44 f(3)(x)
= 60x2 + 24 f(3)(1)
= 84 f(4)(x)
= 120x f(4)(1)
= 120 f(5)(x)
= 120 f(5)(1)
= 120 and f(6)(x) = 0, and the series
terminates. By Taylor’s theorem in (1),
we get: \ x5 + 4x3 + 3x + 1 = 9 + 20(x - 1) +
22(x - 1)2 + 14(x - 1)3 + 5(x - 1)4 + (x -
1)5…… (3) |
|
Example 2 Express in partial
fraction: Solution Using the
technique in the previous example for the numerator of the fraction, from (3)
we get: |
|
Example 3 Express in partial
fraction: Solution This problem
is more complicate since there is one more linear factor in the denominator.
We can handle like this: We can get : x2 º f(x) (x – 2) + A (x –1)4 ………
(4) Put x = 2 in (4), we get A = 4 ………
(5) Substitute (5) in (4) and
change the subject to f(x), we have: Now, since f(x) = -4x3 + 8x2
– 7x + 2, f(1)
= 2 f’(x)
= -12x2 + 16x – 7 f’(1)
= -3 f(2)(x)
= -24x + 16 f(2)(1)
= -8 f(3)(x)
= -24 f(3)(1)
= -24 By
Taylor’s Theorem,
Finally
we get: |