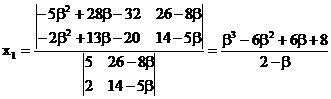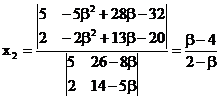Solve two variables order two simultaneous equations

Question

Find the intersection points of :

5x² – 8xy + 5y² + 26x – 28y + 32 = 0

2x² – 5xy + 2y² + 14x – 13y + 20 = 0

Solution

Let (a, b) be the intersection point(s), after substitution, rearrange, we get:

5a² + (26 - 8b)a = -5b² + 28b - 32

2a² + (14 - 5b)a = -2b² + 13b - 20

Put x₁ = a² , x₂ = a, we get a set of simultaneous equations in x₁ and x₂ :

5x₁ + (26 - 8b) x₂ = -5b² + 28b - 32

2 x₁+ (14 - 5b) x₂ = -2b² + 13b -20 (1)

The coefficient determinant of this set of simultaneous equations is:

If b = 2, this coefficient determinant is equal to zero, at this time a satisfies both equations:

5a² + 10a = 4

2a² + 4a = -2

However, there is no real a satisfying the both quadratic equations above.

Therefore b is not equal to 2.

Using Crammer’s rule for (1), we get:

Since x₁ = a² , x₂ = a

Therefore, x₂² = x₁.

Therefore b satisfies the equation :

(2 - b)(b³ - 6b² + 6b + 8) = (b - 4)².

Therefore b is the root of the equation:

b⁴ – 8b³ + 19b² –12z = 0

b (b – 1)( b – 3)( b – 4) = 0

The roots for b are 0, 1, 3, 4 and after finding the corresponding a:

The points are (-2, 0); (-3, 1), (1, 3), (0, 4)

Exercise

Solve the simultaneous equations:

x² – 3xy + 2y² – 16x – 28y = 0

x² – xy – 2y² – 5x – 5y = 0

Answer : (0, 0); (3, -1); (-2, 2)