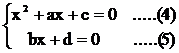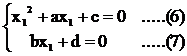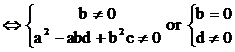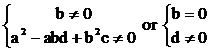Quadratic Equation

 

Introduction

             It is well-known to junior secondary level students that the quadratic equation is of the form:

                    ax2 + bx + c = 0,        where a ¹ 0.

The coefficients a, b, c are real numbers. Here we like to extend to the case of complex numbers.

 

             For simplicity let us begin our equation with:

 

                    x2 + (a + bi)x + (c + di) = 0      , where a, b, c, d Î R                      (1)

 

We assume that equation (1) is a monic (i.e. with coefficient of the term with highest power is 1). If the equation is not monic, we can change it to be monic by division of the first coefficient.

 

Please note that:

(a)  The discriminant of (1),

             D = (a+bi)2 – 4(c+di) 

      is useless in determining the nature of roots as it contains complex numbers.

(b) Complex roots of (1), if exist, may not occur in conjugate pairs as (1) is not an equation with real coefficients.

 

We begin with looking for real roots of (1).

 

Theorem 1

 

             x2 + (a + bi)x + (c + di) = 0      , where a, b, c, d Î R                             (1)

 

      (1) has two real roots (including the case of double real roots)

Û b = d = 0 and a2 – bc ³ 0

 

Proof of theorem 1

 

(Ü)       If b = d = 0, the (1) becomes x2 + ax + c = 0                                          (2)

             Obviously (2) has two real roots (including double roots) since

                    D = a2 – bc ³ 0

 

(Þ)       Let x be the real root of (1).

             (1) can be rewritten in the form:

                    (x2 + ax + c) + (bx + d)i = 0                                                            (3)

 

             We therefore get:

 

                   

 

             If there are two real roots  x1, x2  then from (5),

                    bx1 + d = bx2 + d

                    b(x1 – x2) = 0

             \ b = 0 and hence  d = 0.

             Since (4) has two real roots, therefore  D = a2 – bc ³ 0.

 

Note : (1) has a double real roots   Û         b = d = 0 and a2 – bc = 0

 

Discussion

             Theorem 1 states the fact : If a quadratic equation has two real roots, then the quadratic equation must have real coefficients and we can use the discriminant for quadratic equation with real coefficients to discuss its real roots. If a quadratic has coefficients that are not all real, that is, with complex coefficients, then the quadratic equation does not have two real roots. It has at most one real root and the other root is complex.

 

Theorem 2

 

             x2 + (a + bi)x + (c + di) = 0      , where a, b, c, d Î R                             (1)

 

      (1) has two conjugate complex roots

Û b = d = 0              and        a2 – 4c < 0

 

Proof of theorem 2

 

(Ü)       Obvious follows from the theory of quadratic equation with real coefficients.

 

(Þ)       Let  x1 = m + ni,       x2 = m – ni  where m, n Î R

             be the conjugate roots.

            

             By Vieta theorm,      

                                               Sum of roots = x1 + x2 =  2m = -(a + bi)

                                        Product of roots   = x1x2    = m2 + n2 = c + di

Then we can get, a = -2m, b = 0     and   c = m2 + n2 , d = 0

Now,  a2 – 4c = (-2m)2 – 4(m2 + n2) = - 4n2 < 0

 

     

Discussion

             Theorem 1 and 2 states the fact: In order to determine a quadratic equation having two real roots or two conjugate complex roots, that equation must have real coefficients. We just use the discriminant for quadratic equation with real coefficients to investigate the nature of roots.

 

Theorem 3

             x2 + (a + bi)x + (c + di) = 0      , where a, b, c, d Î R                             (1)

 

      (1) has one real root and one complex roots

Û b ¹ 0  and         d2 – abd + b2c = 0

 

 

Proof of theorem 3

 

(Þ)       Let x1 be the real root, then

                    x12 + (a + bi)x1 + (c + di) = 0

                    (x12 + ax1 + c) + (bx1 + d)i = 0

 

                   

 

             Since there is only one real root, from (7), b ¹ 0 and  x­1 = - d/b                    (8)

             Substitute (8) in (6), and multiply by b2 we get    d2 – abd + b2c = 0.

 

(Ü)       If  b ¹ 0  and  d2 – abd + b2c = 0, then

 

                          

 

             Let   x1 = - d/b, we can check from (9) that x1 satisfies (6) and (7).

 

\       (x12 + ax1 + c) + (bx1 + d)i = 0

\       x12 + (a + bi)x1 + (c + di) = 0

\       x1 is a real root of (1).

 

Finally, we see that there is only 1 real root, because if there are 2 real roots, from theorem 1, b = 0, contrary to the given that b ¹ 0.

                   

 

Discussion

                    This leaves the final case that the quadratic equation has two complex roots in which they are not conjugate pairs. The proof of the theorem 4 below follows easily from theorem 1,2 and 3 and is not given. Hey, guys, it is your turn to provide the logics.

     

 

Theorem 4

             x2 + (a + bi)x + (c + di) = 0      , where a, b, c, d Î R                             (1)

     

Equation (1) has two complex roots which are not conjugate pairs

 

 

 

Summary

 

x2 + (a + bi)x + (c + di) = 0     , where a, b, c, d Î R

Nature of roots

Necessary and sufficient conditions

Two real roots
(include 1 double root)




Two conjugate complex roots




One real root and one complex root




Two complex roots which are not conjugates