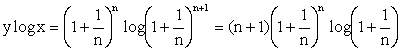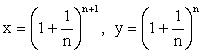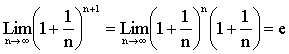Unexpected roots of y^x = x^y
Curious equation : y^x = x^y In this article, we like to solve this equation for different cases. Some techniques of calculus in Advanced Level are needed.
Trivial solutions (1) The non-exciting solutions are y = x. So (x, y ) = (3, 3), (5, 5) are examples. (2) After some trials, perhaps you can get the solutions: (x, y) = (2, 4) and (4, 2). (3) With more calculations, you can reach the solutions: (x, y) = (-2, -4) and (-4, -2). Are there other solutions? We restrict out discussions to positive real x and y below.
The Graph I use Winplot to draw the graph of y^x = x^y. It is of course an implicit function. The graph shows two parts: a straight line showing all solutions for which x = y, and a curve showing all solutions for which x ¹ y. There are two asymptotes for the curve (in which the curve is getting closer and closer to): x = 1 and y = 1. The unexpected root of the equation is where the straight line cuts the curve in the graph: (x, y ) = (e, e). Whew!
Rational Roots Are there any rational roots? We now show that for x > y, where n Î N, are rational roots of the equation. Consider, \ x log y = y log x \ log y^x = log x^y \ y^x = x^y.
Why (e, e) is on the straight line and the curve? It is obvious that (e, e) is on the straight line y = x. In the above, for x > y, where n Î N, are rational roots of the equation and hence on the curve. But we know that from most calculus book: , \ (e, e) is also on the curve.
Irrational Roots We know that e is an irrational number. Is there any other irrational number satisfying the given equation? It is not difficult to check that (3Ö3, Ö3) is on the curve. At this moment you may enjoy showing that: If k is any real number not equal to 1, then: is real number solution by using logarithm.
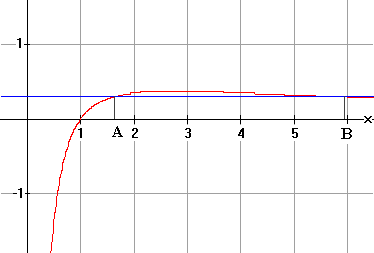
More Graph A different approach by considering: a^b = b^a. b ln a = a ln b So if we plot the graph: Draw any horizontal line : y = c, 0 < c < 1/e The straight line cuts the curve at two points. The x coordinates of these two points gives the solution pair.		The line y = 0.3 cuts the curves. A = 1.63134 B = 5.93779 1.63134^5.93779 = 5.93779^1.63134 » 18.283