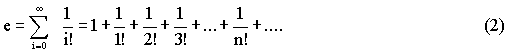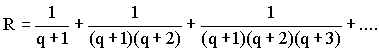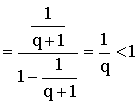e is an irrational number

Introduction

Before we study the proof, you should know:

(a) An irrational number cannot be written in the form p/q where p, q Î Z. q ¹ 0 and

H.C.F. (p, q) = 1.

(b) Infinite Geometric Progression:

(c) e can be expressed as an infinite series :

Proof

Here is not a very difficult proof:

If e = p/q is rational, multiply (2) by q!, we get:

The L.H.S. of (3) is an integer.

The terms in the first bracket of R.H.S. are also integers.

But the terms in the second bracket of R.H.S.

\ R is number between 0 and 1 and is not an integer.

\ There is a contradiction that the L.H.S. of (3) is an integer and the R.H.S. is not.

\ e is an irrational number.