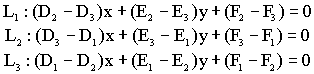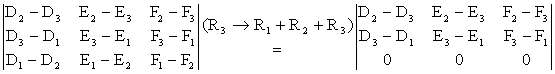|
The
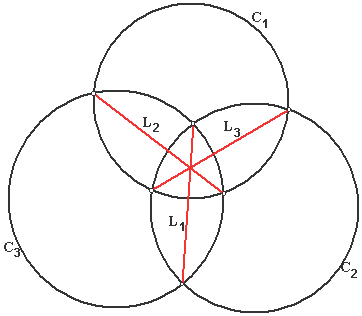
common chords of any three circles |
|
|
Theorem The common chords of any three circles
are concurrent. |
|
|
Proof Here is an
interesting proof using the theory
of determinant. Let the equations of any
three circles be: |
|
|
The three common chords
are : We can then form the
coefficient determinant using these equations: = 0 (since the entries of row 3 are zero) \ |
|
|
Note This theorem is also
true if the circles are not intersecting. In such case, the radical axes have
to
be used instead of the common chords. |
|