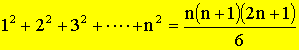Physics method to show this series
As in the diagram on the left, through the point construct a line BC perpendicular to the x-axis. Use as vertex, construct an equilateral triangle . Correspond to the points construct lines perpendicular to x-axis. On place a unit mass. Similarly on the perpendicular lines through place 2, 3, …, n unit masses equidistant apart. We like to use 2 methods to find the total moment correspond to the origin.
Method 1 The total moment is the sum of all the moments of the masses along the vertical lines, that is: \ M = 1 x 1 + 2 x 2 + 3 x 3 + …. + n x n	Method 2 The total moment is equal to the product of the total weight and the center of mass of all unit masses. Now, the center of mass of all unit masses is the center of mass of triangle ABC from the origin. Remember that the center of mass is at two-third of the median of the triangle, therefore we get the distance of center of mass from the origin: And the total mass is:
Joining the results of the two methods, we get: