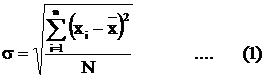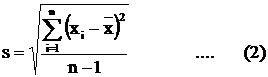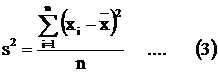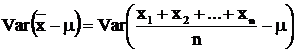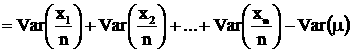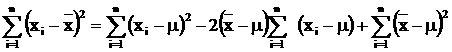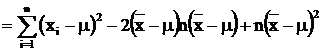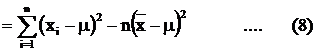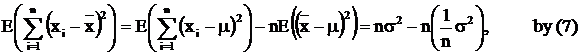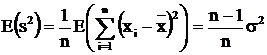|
|
Why we use (n -1) in the
denominator of standard deviation formula ?
|
|
|
|
In short, if
x1, x2 ,…, xN be independent and identically
distributed random variables. The standard deviation of the entire population
is given by the formula :
However, if
x1, x2 ,…, xn ( n < N ) is not a set variables of the entire
population, but only a sample of the population, then we use the
standard deviation formula :
|
|
|
|
Why we do like this ? Not so technical, we use (n – 1) because we just like to make the
"spread" (or deviation) a little larger to reflect the fact that,
since we are using a sample, not the entire population, we have more
uncertainty. |
|
|
|
Degree of freedom Degrees of
freedom is a measure of
how much precision an estimate of variation has. A general rule is
that the degrees of freedom decrease when we have to estimate more
parameters. Before
you can compute the standard deviation, we have to first estimate a mean. This causes you to lose one
degree of freedom and you should divide by (n – 1) rather than n. In more complex situations, like
Analysis of Variance and Multiple Linear Regression, we usually have to
estimate more than one parameter. Measures of variation from these procedures
have even smaller degrees of freedom. |
|
|
|
Unbiased estimator A
more formal way to clarify the situation is to say that s
(or the sample standard deviation) is an unbiased estimator of s
, the population standard deviation if the denominator of s
is (n – 1). Suppose
we are trying to estimate the parameter
Q using
an estimator θ
(that is, some function of the observed data). Then the bias of θ
is defined to be
E(θ) – Q , in
short, "the expected value of the estimator Q
minus the true value θ .
" If E(θ) – Q = 0 , then the estimator is unbiased. |
|
|
|
Variance formula using
n instead of (n – 1) is biased Suppose we use the variance formula (square of
standard deviation) We are going to show that Since
E(s2) ¹ s2 , s2 is a biased estimator of s2 if we
use (3) instead of (2). |
|
|
|
Prerequisite We would like to clarify some points before we like to
prove (4) . Firstly, if
X and Y
are independent and identically distributed, we have: Var (kX) = k2
Var (X) .... (5) Var (X + Y) = Var (X) + Var (Y) .... (6) The proofs of (5) and (6) are left to the reader. Secondly, if since x1 , x2 , …, xn are independent and identically distributed and having the same variance s2 . |
|
|
|
Proof of (2)
Taking the summation, we
have Taking the expection of (8),
|
|