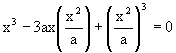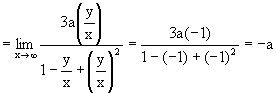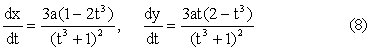Sketch a graph with implicit equation

Problem

Sketch the graph : x³ – 3axy + y³ = 0 (*)

Click here to open a window to show the final sketch of the graph. Minimize, open, or resize the window so that you can check at various discussions below.

Intercept, domain, range, periodicity

The curve cuts at the point (0, 0).

Domain (-¥, +¥)

Range (-¥, +¥)

The function is not periodic.

Symmetry

(1) Replace x by (– x) in (*), (*) is not unchanged. Therefore (*) is not symmetric about y-axis.

(2) Replace y by (– y) in (*), (*) is not unchanged. Therefore (*) is not symmetric about x-axis.

(3) Replace x by (– x) and in (*), y by (– y) in (*). The equation is unchanged.

Therefore the equation is symmetric about the line

Derivatives

x³ – 3axy + y³ = 0 (*)

Differentiate (*), we get: 3x² –3axy’ – 3ay + 3y²y’ = 0

The second derivative is difficult to find.

Differentiate (1), we get:

Substitute (1) in and simplify,

Getting the second derivative seems not very helpful in sketching this graph.

Turning points

For turning points, put the first derivative to zero.

From (1), we get ay – x² = 0

y = x²/a (3)

It seems to get into trouble since we want the value(s) of x.

Luckily we have the original equation!

Substitute (3) in (*), we have:

x⁶ – 2a³x³ = 0

x³(x³ – 2a³) = 0

Testing for local maximum or minimum for (4) is not easy.

It is also not easy to find the corresponding value of y for, because after you substitute this value to (*), you get a cubic equation. (You may try!)

Later, we know that y is a local maximum when and a local minimum when x = 0.

Asymptotes

There are no horizontal or vertical asymptotes. For oblique asymptote, y = mx + c

x³ – 3axy + y³ = 0 (*)

Take x®¥, 1 – 3a(0)m + m³ = 0

m³ + 1 = 0

\ m = -1.

\ The oblique asymptote is y = -x – a.

Parametric equation

Let y = xt (5)

Substitute in x³ – 3axy + y³ = 0 (*)

We get, x³ – 3ax(xt) + (xt)³ = 0

x³ – 3ax²t + x³t³ = 0

x(1 + t³) = 3at

Subst. (6) in (5),

Please note:

(1) Parametric form can give you more insight in sketching the curve, which is discussed later.

(2) Equation (5) is only a good try to change an implicit equation to parametric form. The method
is not universal.

(3) It is very interesting to see where the point (x, y) lies for different values of t:

t	-¥	(-¥, -1)	-1^-	-1^+	(-1, 0)	0	(0, +¥)	+¥
x	0	+	+¥	-¥	-	0	+	0
y	0	-	-¥	+¥	+	0	+	0

Derivatives

You may check the following:

and from this you can get:

Tables

The table of first derivatives can give you a lot of hints in sketching the curve. The second derivatives give you even more information. (The second derivative is not discussed here.)

t	(-¥, -1)	-1	(-1, 2^-1/3)	2^-1/3	(2^-1/3, +¥)
	+	undefined	+	0	-

t	(-¥, -1)	-1	(-1, 0)	0	(0, 2^1/3)	2^-1/3	(2^1/3,+¥)
	-	undefined	-	0	+	0	-

t	(-¥, 0)	0	(0, 2^-1/3)	2^-1/3	(2^-1/3, 2^1/3)	2^1/3	(2^1/3,+¥)
	-	0	+	undefined	-	0	+

These tables give you the rate of change of x with t, rate of change of y with t and rate of change of y with x. Investigate the turning points using the above tables.

Asymptote re-visited

From the parametric form:

\ The oblique asymptote is y = -x – a, the same as before.