Roots, Asymptotes and Holes of Rational functions

What is rational function ?

A rational function is a function that can be written as a fraction of two polynomials where the denominator is not zero.

Domain

The domain of a rational function is all real values except where the denominator, q(x) = 0

Example

Find the domain of :

Solution

Domain = {(-¥, 1) È (1, 2) È (2, +¥)}

Roots

The roots (zeros, solutions, x-intercepts) of the rational function can be found by solving:

p(x) = 0

This roots can be found usually by factorizing p(x). If the multiplicity of a factor (x - c) is odd, the curve cuts the x-axis at x = c. If the multiplicity of a factor is even, then the curve touches the x-axis at x = c.

We shall discuss the case in which (x – c) is both a factor of numerator and denominator.

Vertical Asymptotes

An asymptote is a line that the curve goes nearer and nearer but does not cross. The equations of the vertical asymptotes can be found by solving q(x) = 0 for roots. We shall study more closely if some roots are also roots of p(x) = 0.

If you write p(x) in factorized form, then you can tell whether the graph is asymptotic in the same direction or in opposite directions by whether the multiplicity is even or odd.

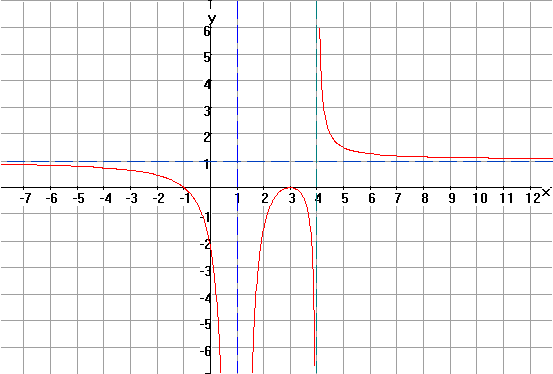
Asymptotic in the same direction means that the curve will go up or down on both the left and right sides of the vertical asymptotes. Asymptotic in opposite direction means that the one side of the curve will go down and the other side of the curve will go up the vertical asymptotes.

Example

(1) The curve cuts the x-axis at x = -1 since the multiplicity of (x + 1) is 1, which is odd.

The curve touches the x-axis at x = 4 since the multiplicity of (x -3) is 2, which is even.

(2) The curve is asymptotic in the same direction of x = 1, since the multiplicity of (x – 1) is 2.

The curve is asymptotic in opposite direction of x = 4, since the multiplicity of (x – 4) is 1.

Horizontal asymptotes

A horizontal asymptote is a horizontal line which the curve approaches at far left and far right of the graph.

The location of the horizontal asymptote is found by looking at the degrees of the numerator (n) and the denominator (m).

(1) If n < m, the x-axis (or y = 0) is the horizontal asymptote.

(2) If n = m, then y = a_n / b_m is the horizontal asymptote. (ratio of the leading coefficients)

(3) If n > m, then there is not horizontal asymptote.

In the above graph, the horizontal asymptote is x = 1. Note that the curve is asymptotic at opposite side of the line x = 1. It can be asymptotic in the same direction depending on the given curve. Rational function has at most one horizontal asymptote. Other function may have more than one horizontal asymptote.

Hole

Sometimes, a factor may appear in both the numerator and denominator. Let us assume that the factor (x – c)^s is in the numerator and (x – c)^t is in the denominator.

(1) s < t, then there will be a vertical asymptote x = c.

(2) s > t, then there will be a hole in the graph on the x-axis at x = c. There is no vertical asymptote there.

(3) s = t, then there will be a hole in the graph at x = c, but not on the x-axis. The y-value of the hole can be found by canceling the factors and substituting x = c in the reduced function.

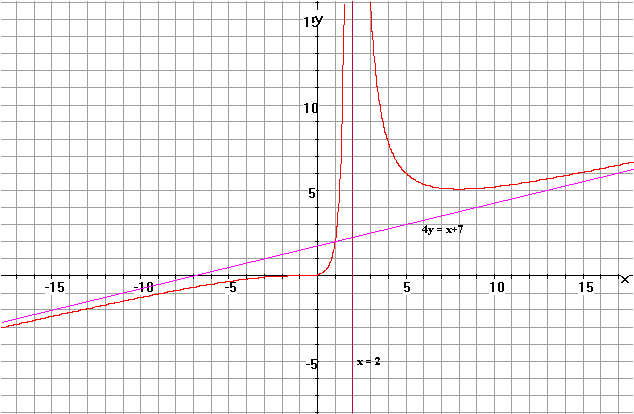
Oblique Asymptote

When the degree of the numerator is exactly one more the degree of the denominator, the graph of the rational function has an oblique asymptote. In other cases, there will be no oblique asymptote.

The equation of the oblique asymptote can be found by division.

Example

										1	+	7
1	-	4	+	4	)	1	+	3	+	3	+	1
						1	-	4	+	4
								7	-	1	+	1
								7	-	28	-	28
										27	-	27

By division, we get

\

or 4y = x + 7 is an oblique asymptote.

and x = 2 is a vertical asymptote.