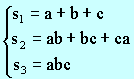Polynomial Equations for Sum of Square Roots

Given an arbitrary integer “a”, which is not a complete square.

We can find the minimal polynomial with integer coefficients and having the root:

This can be easily done by squaring both sides and we can get:

This equation has two roots, namely,

Given two arbitrary integers “a” and “b”, which are not complete squares.

We can find the minimal polynomial with integer coefficients and having the root:

This can be easily done by squaring both sides and we can get:

Subtract a + b from both sides, square both sides again, and rearrange the terms, we get the polynomial equation :

This equation is of degree 4 and has 4 roots, namely:

If we begin with three integers “a”, “b” and “c”, not complete squares, and we wish to find a polynomial equation with integer coefficients having one of the roots :

………. (1)

To simplify our work we define the symmetric functions :

………. (2)

Square both sides of (1) and rearranging, we get:

….. (3)

Square (3) again, we have:

Make use of (2) and rearranging, we therefore get:

Square again,

Note that this expression contains radicals similar to (3) and can be replaced by the left hand side of (3). We finally arrive at the polynomial equation with some rearrangement of terms:

……… (4)

Equation (4) is of order 8 and has 8 roots, namely:

Example

Find the minimal polynomial equation with root:

Now,

By (4), the polynomial equation is:

or

………. (5)

Finale

I put equation (5) in MATHEMATICA, and it gives another form in one of the solutions:

Can you show that this root is identical to :

?