Experimental method to find π
Have you ever thought that π can be found by throwing matches? It seems ridiculous, isn’t it? But an Italian mathematician, Lazzerini, really use this method to find π and the calculated π agreed quite well with the actual theoretical value (3.1415926535…)
To find π by this method, you should have a large piece of paper with parallel lines separated at a distance equal to the length of the matches, as in the diagram in the left. Now, for simplicity, take this length to be 2 units. Then you have to throw the matches on to the paper. π can be calculated by:
Link This experiment is called Buffon’s needle. You can follow this link to do this interesting experiment: http://www.metablake.com/pi.swf
The reason The ways in which matches fall on parallel lines can be determined by: 1. the distance between the lines and the center of the matches; 2. the angle between the lines and the matches as shown in the figure.
If a match with greater angle θ and is close to the line, intersection occurs (match a), otherwise, there is not intersection (match b). To be more specific, if the vertical projection is greater than the distance between the line and the center of the match, intersection occurs.
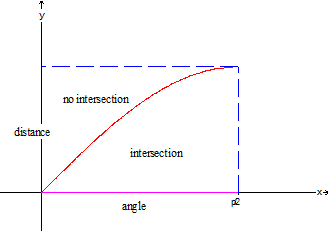
This idea can be generalized by the graph of distance against angle as shown in the figure on the left. It is in fact a sine curve as the vertical projection is 1×sin θ. (The whole match has length 2 units) From the theory of probability, we know that probability of intersection
We take the angles from 0 to π/2, the same is for π/2 to π. Shaded area Whole area \ The probability of intersection
Lazzerini had thrown 3408 matches of which 2169 matches intersected the lines, hence: which is correct up to the sixth decimal places!