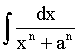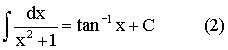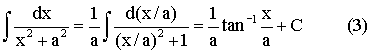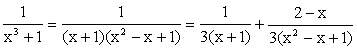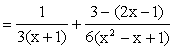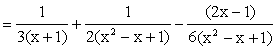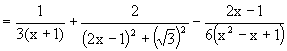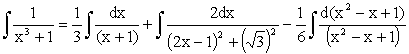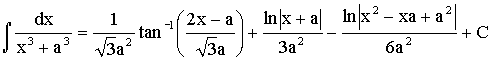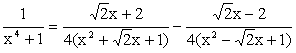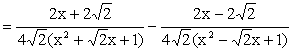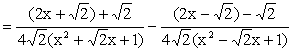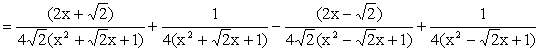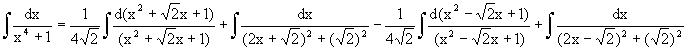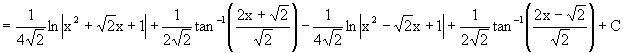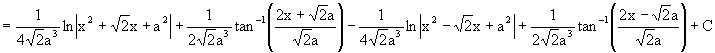Example of using Partial Fraction to evaluate Integral |
|
|
Problem We
like to evaluate the integral: where n = 1, 2, 3, 4. We employ the technique of
Partial Fractions. This algebraic method is assumed to be known. |
|
|
When n = 1, |
|
|
When n = 2, By using the substitution x = tan q, it is a simple exercise
to get: Then, In getting (3) here, we
change the variable and apply (2). Alternatively, you can
start by using the substitution x = a tan q at the beginning of (3). |
|
|
When n = 3,
|
A Partial Fraction exercise! Second fraction is further broken. Note : d(x2 – x + 1) = 2x – 1 Use completing square in the denominator of the second
fraction. In the second integral, you may use 2x – 1 = Ö3 tan q to evaluate. |
|
Finally you may check by
changing the valuable suitably:
|
|
|
When n = 4, Since x4 + 1 cannot be
factorized under rational numbers, we start with the factorization : x4 + 1 = (x4
+ 2x2 + 1) – 2x2 = (x2 + 1)2 – (Ö2 x)2 = (x2
+ Ö2 x + 1)(x2
-Ö2 x +1) As a Partial Fraction
exercise, we get:
Finally, if you still feel
energetic of checking, we arrive:
|
|