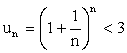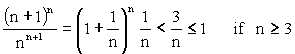An application of Mathematical Induction to Inequality

Problem

Prove that :

Mathematical Induction

The use of Mathematical Induction to prove

(1)

is difficult. So we would like to change the proposition to:

nⁿ⁺¹ > (n + 1)ⁿ , " n ³ 3 (2)

However, the change does not improve much! You may try before you carry on.

Change of Proposition

It is interesting that you can change the proposition to :

P(n) : v ³ n ³ 3, nvⁿ > (v + 1)ⁿ.

Induction on n.

Proof:

For P(3), 3v³ = v³ +v³ + v³ ³ v³ + 3v² + 9v (since v ³ 3)

= v³ + 3v² + 3v + 6v

> v³ + 3v² + 3v + 1

= (v + 1)³.

\ P(3) is true.

Assume P(k) is true for some k, where v ³ k ³ 3,

that is, kv^k > (v + 1)^k…… (*)

For P(k + 1), (k + 1)v^k+1 = (k + 1) v v^k = (kv + v) v^k

³ (kv + k) v^k

= (v + 1) kv^k

> ( v + 1)(v + 1)^k, by (*)

= (v + 1)^k+1.

\ P(k + 1) is also true.

By the Principle of Mathematical Induction, P(n) is true "nÎN, where v ³ n ³ 3.

Hey, my friend. The proof is complete by putting v = n. Check this!

Another viewpoint

In the discussion of the constant e in most textbook, the sequence

is shown to be bounded and monotonic increasing.

If we assume that

is proved, then this problem can be solved easily.

Applying this,

Hence (2) is proved. Result follows!