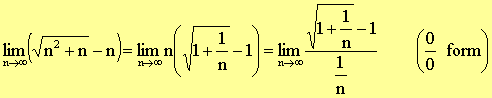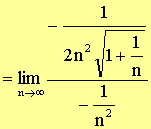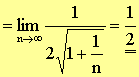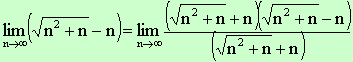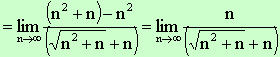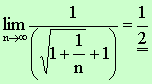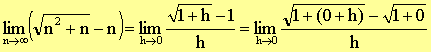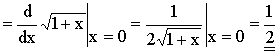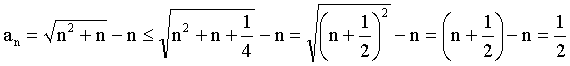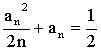An example in using L’hospital Rule

The Problem

Use L’hospital Rule to show that:

Go L’hospital

, applying L’ hospital rule

Fun with rationalization

Algebra method is even better for this problem.

, rationalization of numerator!

Differentiation is an unexpected way

Put ,

As n ® ¥, h ® 0.

(Wow! Fun!)

More involved calculations using “Bounded monotone theorem”

………. (1)

(Boundedness)

(Monotonic increasing)

4n²+4n+1 > 4n²+4n

(It is important to note that the “thinking steps” and the “working steps” in the above are in reverse order!)

(The limit)

From the above, by the Bounded monotone theorem, the limit exists.

Let

From (1),

a_n² + 2na_n + n² = n² + n

Taking limit n ® +¥ , we can get:

Haha! Calculations are long, not for the chicken heart!