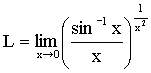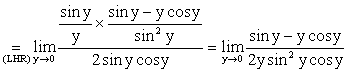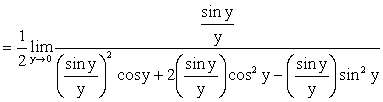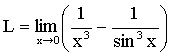Harder problems of L’hospital rule

Problem 1

Evaluate the limit:

Analysis

The difficult part is the sin^-1x inside the function. Even if you take the logarithm of L and apply L’hospital rule, the limit cannot be evaluated easily.

Solution

The trick is to change the variable.

Let y = sin ^-1x, then sin y = x. As x ® 0, y ® 0.

Calculations

Problem 2

Evaluate the limit:

Analysis

You may join the fractions in L. However, you need to apply L’hospital rule three times and the evaluation is lengthy.

Solution

The point is to apply the formula: a³ – b³ = (a – b)³ +3(a²b - ab²)

Then:

Note that we changed the denominator of L₂ to double angle for easier differentiation.

By applying L’hospital rule twice to each of L₁ and L₂ (calculations are left to the reader), we can get L₁ = 0, L₂ = ¥ and L = ¥.