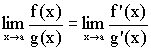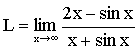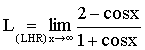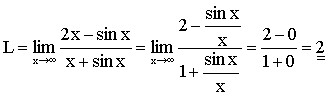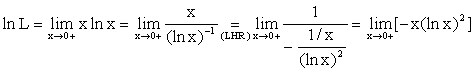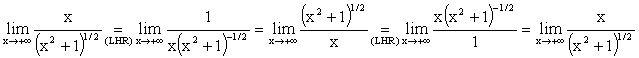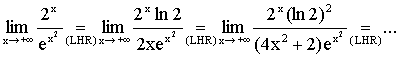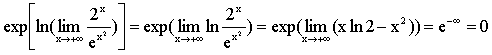Some Points to Note in L’hospital Rule |
||||||||
|
Summary of
L’hospital Rule
Let
f and g be differentiable on an interval I containing the point a (except may
be point a itself) and let g’(x) ¹ 0 on I \{a}. If provided the right hand
side limit exists (or equal to +¥, -¥). Note that the rule can
also be applied to one-sided limit (x®a+, x®a-) as well as
infinity (x®+¥, x®¥) |
||||||||
|
Nonexistence
of RHS of (*) does not prove the nonexistence of LHS of (*) Consider: It is of ¥ ¤ ¥ form, if you apply
L’hospital rule (LHR), you get: Since cos x does not have
a limit as x®¥, the limit on RHS does
not exist. In fact, the limit L
really exists, since sin x is bounded, we have |
||||||||
|
Algebra
Some algebra is needed to
change other indeterminate forms to the basic quotient form. In the
followings the ‘0’ and ‘¥’ are
“functions”. Product form: Difference form: Power form: Take
logarithm, then reduce to Product Form and then Quotient Form. |
||||||||
|
Example (1) which
is more complicate than the original problem. (2) \ L = e0 = 1 |
||||||||
|
Interesting cases (1) Applying the L’hospital rule (LHR)
below: The
result is cyclic! In fact, we may evaluate as follows: (2) which cannot yield any result. But by taking logarithms, we
get: |