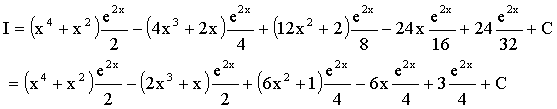Extending Integration by parts

Integrals of the form where u(x) is a polynomial and v(x) is a function that can be differentiate repeatedly (e.g. sin x, cos x, ) are often evaluated by repeated integration by parts. It is found that tabular layout can be useful in finding such integrals.

Example 1

Sign	Derviatives	Integrals
	u ‾ v ®	sin x
+		-cos x
-		-sin x
+		cos x
-		sin x
+	120x	-cos x
-	120	-sin x

Example 2

Sign	Derviatives	Integrals
	u ‾ v ®
+
-
+
-	24x
+	24

For more serious learner :

The integration by parts formula :

can be found in most calculus books and is not repeated here.

Let u₀ = u and u₁ be the first derivative of u.

Let v₀ = v and v₁ be the anti-derivative (integral) of v.

then (1) can be written in the form :

Now, suppose that the function f can be differentiated n-times and

let u_i ( i = 1, 2, …. , n ) be the i-th derivative of u.

Also suppose that the function g can be integrated n-times and

let v_i ( i = 1, 2, …. , n ) be the i-th anti-derviative of v.

The formula (2) can then be extended to the form :

If u_n = 0, then (3) can be simplified to the form

The formula in (3) can be proved by applying to (2) the integration by parts (n-1) times more, or more strictly, by using mathematical induction. The proof is left to the reader.