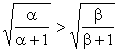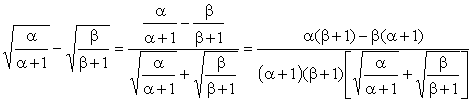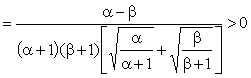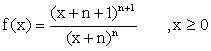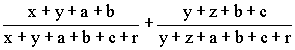Examples in using Increasing and decreasing function
Theorem of Interest Most advanced level students know this: Let f(x) be continuous on [a, b] and differentiable on (a, b). Then (a) if f ’(x) > 0, "x Î (a, b), f(x) is strictly increasing on [a, b]; (b) if f ’(x) < 0, "x Î (a, b), f(x) is strictly decreasing on [a, b]. The following examples illustrate the applications of this theorem to inequalities.
Example 1 Show that if a > b ³ 0, (Method 1) Difference method Result follows. (Method 2) Quotient method Result follows. (Method 3) Calculus method \ f(x) is an increasing function. \ f(a) > f(b) , if a > b ³ 0 Result follows.
Example 2 Given that a real number r with 0 < r < 1, show that 0 < x £ 1 (1 + x ) ^r < 1 + rx The solution involves the construction of a function: f(x) = 1+ rx – (1 + x)^r Then f ’ (x) = r [1 - (1 + x)^r-1 ] < 0 since r – 1 < 0 and (1 + x ) > 1. \ f(x) is increasing. f(0) = 0 \ f(x) < 0 " xÎ (0, 1) \ (1 + x ) ^r < 1 + rx
Example 3 The construction of a function may not be so straightforward as in example 2. To prove that: The construction of the function : and showing that : will gives f(x) an increasing function. The reader can verify the proof by noting f(1) > f(0). If you are more mathematical mature, investigate how f(x) is constructed.
Example 4 Even more difficult example involves the use of the concept of increasing function together with other principles. For x, y, z, a, b, c, r > 0, prove that:
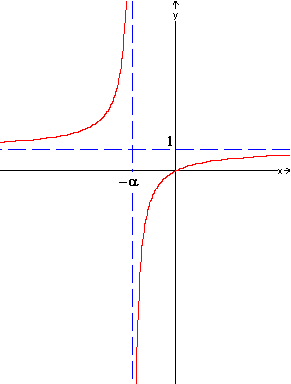
Seems nowhere to go. But by constructing By differentiation (omit here), we can show that f(x) is increasing on (-¥,-a) (-a, +¥). Motivated reader may even show that the graph is a hyperbola. Using this increasing property, we get: