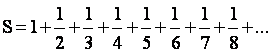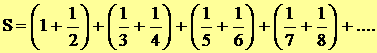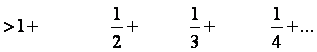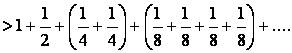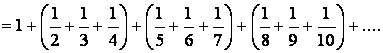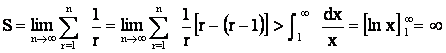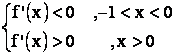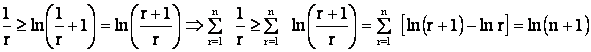Harmonic series

The harmonic series

is divergent.

Proof 1

If not, it converges to a finite sum S , then

\ S > S

Contradiction!

Proof 2

= ¥

Proof 3

First consider:

Then, if S is finite, we have

= 1 + S

Contradiction !

Proof 4

A short calculus proof using definite integral,

\ S is divergent.

Proof 5

Another proof using differentiation .

First we like to prove that : x ³ ln (x + 1) for all x > –1 .

Let f(x) = x – ln (x + 1)

\ f(x) is a minimum at x = 0

\ f(x) ³ f(0) = 0 Þ x ³ ln (x + 1)

Next, we put x = 1/r

\ S is divergent.

Proof 6

First consider :

\ S is divergent.

Proof 7

If

where S is finite.

then

The sum of the odd terms must be the other half:

However this is impossible since for all positive integer, we have :

The contradiction concludes the proof.