Can we draw an equilateral triangle on geo-board?
Geo-board problem A geo-board is used in primary school mathematics learning. It is composed of nails or pegs forming a lattice of squares as in the right diagram. Students can use rubber bands to enclose geometric figures. The problem is : can you enclose an equilateral triangle using rubber bands? (The geo-board is supposed to be large enough to have as many points as we wish and the equilateral triangle can be of any size.)
Try to make an equilateral triangle with a geo-board Click here to open a java geo-board and try to make an equilateral triangle. Is it possible?
Solution I think you cannot make an equilateral triangle. How can we prove this? We can answer this using co-geometry. Here we simply use the concept of rotation of vector.
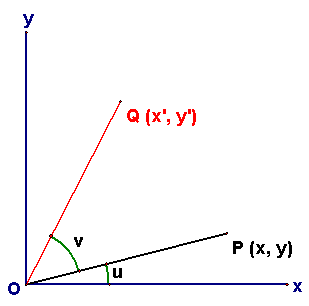
Rotation of vector Use the origin as the center of rotation. Rotate the vector OP(___) by the angle v to OQ(___), where Ðv > 0 for rotating anti-clockwisely and Ðv < 0 for rotating clockwisely. If P = (x, y) and Q = (x’, y’), find x’, y’ in terms of x , y. Let u be the Ð of inclination of OP(___). Then u + v is the Ð of inclination of OQ(___).
\ x’ = projection of OQ(___) on Ox = OQ cos (u + v) = OP cos (u + v) = OP [cos u cos v – sin u sin v] = (OP cos u) cos v – (OP sin u) sin v = x cos v – y sin v	y’ = projection of OQ(___) on Oy = OQ sin (u + v) = OP sin (u + v) = OP [sin u cos v + cos u sin v] = (OP cos u) sin v + (OP sin u) cos v = x sin v + y cos v
Equilateral triangle on geo-board problem Firstly we move one of the vertices of the triangle to the origin O. Let OP be one of the arms of the triangle. Then, P = (x, y), where x, y must be integers. Since P can only on x or y axis, but not both, therefore x and y cannot equal to zero simultaneously. Since we want an equilateral triangle OPQ, rotate OP to OQ by 60°. Q = (x’, y’). Then, Since (i) x, y must be integers, (ii) x and y cannot equal to zero simultaneously, (iii) Ö3 is an irrational number and is not an integer, therefore at least one of x’, y’ must be an irrational number. We have the conclusion that Q must not be one of the points on the geo-board and the proof is complete!