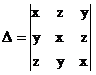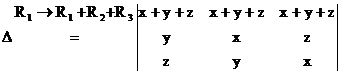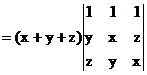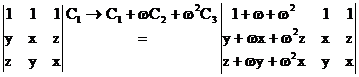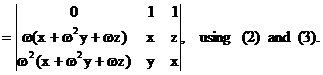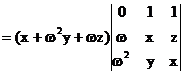Factorize : x³+y³+z³ – 3xyz

Introduction

The factorization

x³ + y³ + z³ – 3xyz = (x + y + z)(x + wy + w²z)(x + w²y + wz) (1)

where w is the complex cube root of unity.

can be proved by direct expansion of the right hand side, starting easier by multiplying the last two factors first. The following is an interesting method to factorize the expression, using determinant.

Points to note

Since w is the cube root of unity, we have

w³ = 1 (2)

Also,

Factorization

Consider

By direct expansion, we can get D = x³ + y³ + z³ – 3xyz

The trouble is the last determinant, if we expand this determinant directly we can only get the factorization:

D = x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)

Further factorization

= (x + w²y + wz) [( -w - w²)x + wy + w²z]

= (x + w²y + wz)( x + wy + w²z) since 1 = -w - w², by (3)

Therefore we can get (1) accordingly.