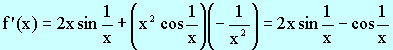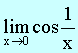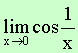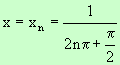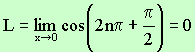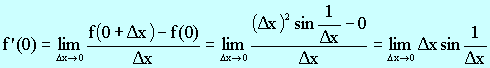Spot the mistake in Differentiation

Question

Let

find f’(0), if exists.

“Supposed solution”

For x ¹ 0,

Since does not exist, (see note below)

\ does not exist.

\ f ’ (0) does not exist.

Anything wrong?

Note

L = does not exist:

Choose , then

Choose , then

\ L does not exist since “limit, if exists, must be unique.”

Solution

,

= 0 as

For smart mathematician like you

For this function f(x) in this question:

(1) Is f(x) continuous at x = 0?

(2) Is f ’(x) continuous at x = 0?

(3) Does f ”(x) exist?

Enjoy your investigation!